Jarhyn
Wizard
- Joined
- Mar 29, 2010
- Messages
- 14,488
- Gender
- Androgyne; they/them
- Basic Beliefs
- Natural Philosophy, Game Theoretic Ethicist
Ok, another weird thread documenting my strange journey through number theory: Exactly How many primes are there in a region of numbers?
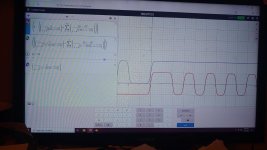
This is a strange one and requires a visualization of the patterns that exist in the Sieve of Eratosthenes to understand. Also, I might add, I wasn't expecting this but I started getting vibes from the movie Pi.
For a given N, lets ask "how many primes are there less than".
Lets start with 4.

I've graphed out some iterations of sin(x*pi/P)/n(P) By counting all primes mapped (1 of them, not counting "1"), we get a number: 3-1.
Lets estimate the number of primes, then, under 12. For that, it looks like the number is 7-1. so, 6.
That's wrong though. It's off by 1.
It breaks down once the calculation reaches the first square of the first prime that is not exactly known: 9.

Now, as you can see, I've added another line. This represents another step: reducing the error.
To reduce the error, you need to find the COUNT of cross products and power products. To do this, I start squaring primes, and for every square and cross product less than 12, I can subtract 1 from my estimation. So, 6-1 is 5. Hooray, I have corrected my error.
There are 5 primes under 12, and 4 remaining lines. For regions above 12, it appears that there are "about" 4 primes per segment.
Between 0 and 60, there are "about" 5+4*(5-1) primes. so 21. This is wrong though. It's off by a few.
To correct the error, we need to figure out a couple more primes, though that's easy because the tool we use to get the estimate has already revealed them in it's pattern because this system will always locate all primes quickly under (highest solved)^2. To know how many primes worth of error we have exactly, we need to know the last prime less than square root of 12, which is 3. There is only one of them, so our error is 1.
I can then say "primes 5 and 7, but not 11, square less than 60." This is 2, with a single cross product, so 3; My estimate is wrong by 3. 21-3 is 18. There are 18 primes under 60. I don't really know what they are. For using this system to find out how many primes are OVER 60, however, I'm going to only subtract 5 and its powers under 60, which is 2. Why? Because I haven't gotten to 420 yet, and this describes my estimator for this epoch. so while I know there are exactly 18 primes under 60, I'm going to estimate that there are 16 primes for every region over 60.
Lets estimate using this count out to 420! 18+16*(7-1) gives us roughly 114. But there's an error again
Now our corrective primes do not include 5: We have accounted for this with our "exact count under 60." To resolve the error, we need to again subtract an exact number of primes' cross products and powers. To do this we are going to subtract from our inaccurate estimate "primes greater than 5 whose cross products are less than 420". This means calculating all primes again whose squares are less than 420, and then counting their cross products less than 420. I know the primes in question are 7, 11, 13.
7*7, 11*7, 13*7, 11*11, 11*13, 13*13.
In this part of the problem it is factorial. It will not exactly remain this way: This table becomes large, as if one of the primes in this epoch were to have a square whose product with another prime in the epoch is less than the target number, that also would be an error term. It isn't yet, but it will be. To fix this, we will have to add every "power" of a prime, in addition to the primes themselves, whose value is less than the greatest prime whose square is less than the doubled primorial being observed to the list of "error terms to cross-productize".
at any rate, we have identified our error as 6. There are exactly 108 primes less than 420. Again, because I haven't gotten to 4620 yet, I'm again only going to correct it for 7. This is again because this is where the pattern repeats exactly on the sieve. There are THREE powers of 7 less than 420, so 3. so while there are exactly 108 primes less than 420, for every region OVER 420, there are going to be "about" 108-3, so 105.
Lets do 4620. There are 108 primes less than 420, and for every region of 420 numbers greater than, there are "about" 105 primes. That's going to be about 108+105*(11-1) =1158...
This is a strange one and requires a visualization of the patterns that exist in the Sieve of Eratosthenes to understand. Also, I might add, I wasn't expecting this but I started getting vibes from the movie Pi.
For a given N, lets ask "how many primes are there less than".
Lets start with 4.

I've graphed out some iterations of sin(x*pi/P)/n(P) By counting all primes mapped (1 of them, not counting "1"), we get a number: 3-1.
Lets estimate the number of primes, then, under 12. For that, it looks like the number is 7-1. so, 6.
That's wrong though. It's off by 1.
It breaks down once the calculation reaches the first square of the first prime that is not exactly known: 9.

Now, as you can see, I've added another line. This represents another step: reducing the error.
To reduce the error, you need to find the COUNT of cross products and power products. To do this, I start squaring primes, and for every square and cross product less than 12, I can subtract 1 from my estimation. So, 6-1 is 5. Hooray, I have corrected my error.
There are 5 primes under 12, and 4 remaining lines. For regions above 12, it appears that there are "about" 4 primes per segment.
Between 0 and 60, there are "about" 5+4*(5-1) primes. so 21. This is wrong though. It's off by a few.
To correct the error, we need to figure out a couple more primes, though that's easy because the tool we use to get the estimate has already revealed them in it's pattern because this system will always locate all primes quickly under (highest solved)^2. To know how many primes worth of error we have exactly, we need to know the last prime less than square root of 12, which is 3. There is only one of them, so our error is 1.
I can then say "primes 5 and 7, but not 11, square less than 60." This is 2, with a single cross product, so 3; My estimate is wrong by 3. 21-3 is 18. There are 18 primes under 60. I don't really know what they are. For using this system to find out how many primes are OVER 60, however, I'm going to only subtract 5 and its powers under 60, which is 2. Why? Because I haven't gotten to 420 yet, and this describes my estimator for this epoch. so while I know there are exactly 18 primes under 60, I'm going to estimate that there are 16 primes for every region over 60.
Lets estimate using this count out to 420! 18+16*(7-1) gives us roughly 114. But there's an error again
Now our corrective primes do not include 5: We have accounted for this with our "exact count under 60." To resolve the error, we need to again subtract an exact number of primes' cross products and powers. To do this we are going to subtract from our inaccurate estimate "primes greater than 5 whose cross products are less than 420". This means calculating all primes again whose squares are less than 420, and then counting their cross products less than 420. I know the primes in question are 7, 11, 13.
7*7, 11*7, 13*7, 11*11, 11*13, 13*13.
In this part of the problem it is factorial. It will not exactly remain this way: This table becomes large, as if one of the primes in this epoch were to have a square whose product with another prime in the epoch is less than the target number, that also would be an error term. It isn't yet, but it will be. To fix this, we will have to add every "power" of a prime, in addition to the primes themselves, whose value is less than the greatest prime whose square is less than the doubled primorial being observed to the list of "error terms to cross-productize".
at any rate, we have identified our error as 6. There are exactly 108 primes less than 420. Again, because I haven't gotten to 4620 yet, I'm again only going to correct it for 7. This is again because this is where the pattern repeats exactly on the sieve. There are THREE powers of 7 less than 420, so 3. so while there are exactly 108 primes less than 420, for every region OVER 420, there are going to be "about" 108-3, so 105.
Lets do 4620. There are 108 primes less than 420, and for every region of 420 numbers greater than, there are "about" 105 primes. That's going to be about 108+105*(11-1) =1158...