SLD
Contributor
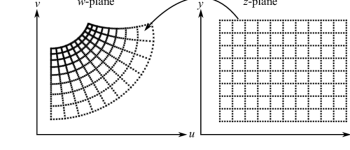
When I create a simple vector field in my WolframAlpha App - the free version for iPad, it creates a diagram of vectors which is the usual way that such fields are Expressed. But I find this too confusing. I was looking for an app or website that would show how a map of how the X,y grid is transformed. Or also how other simple equations are transformed, say a parabola or a circle.
So take a simple vector field say (x^2y, y^2,x). how does it transform x,y in one coordinate system to the next. What happens to a unit circle centered around the point (3,4)? Or a simple parabola y=x^2.
I wouldn’t think it would be so hard to make. But google is not helpful.
TIA.
SLD
So take a simple vector field say (x^2y, y^2,x). how does it transform x,y in one coordinate system to the next. What happens to a unit circle centered around the point (3,4)? Or a simple parabola y=x^2.
I wouldn’t think it would be so hard to make. But google is not helpful.
TIA.
SLD