steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
A thread for real world applications.
Anything I post will be in Scilab. It is free and an easy install.
Anything I post will be in Scilab. It is free and an easy install.
I'm pretty sure ordinal data midpoint of 50% would be described as median rather than mean. Although I do follow to what you are driving.
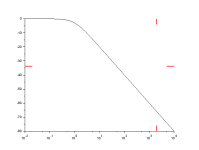
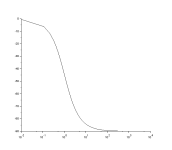
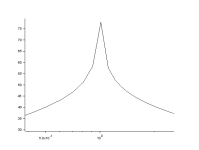
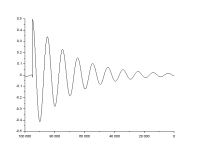
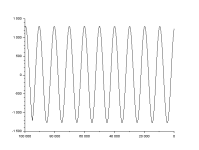
An ideal impact to a structure is a perfect impulse, which has an infinitely small duration, causing a constant amplitude in the frequency domain; this would result in all modes of vibration being excited with equal energy. The impact hammer test is designed to replicate this; however, in reality a hammer strike cannot last for an infinitely small duration, but has a known contact time. The duration of the contact time directly influences the frequency content of the force, with a larger contact time causing a smaller range of bandwidth. A load cell is attached to the end of the hammer to record the force. Impact hammer testing is ideal for small light weight structures; however as the size of the structure increases issues can occur due to a poor signal to noise ratio. This is common on large civil engineering structures.
The Nyquist–Shannon sampling theorem is a theorem in the field of signal processing which serves as a fundamental bridge between continuous-time signals and discrete-time signals. It establishes a sufficient condition for a sample rate that permits a discrete sequence of samples to capture all the information from a continuous-time signal of finite bandwidth.
Strictly speaking, the theorem only applies to a class of mathematical functions having a Fourier transform that is zero outside of a finite region of frequencies. Intuitively we expect that when one reduces a continuous function to a discrete sequence and interpolates back to a continuous function, the fidelity of the result depends on the density (or sample rate) of the original samples. The sampling theorem introduces the concept of a sample rate that is sufficient for perfect fidelity for the class of functions that are band-limited to a given bandwidth, such that no actual information is lost in the sampling process. It expresses the sufficient sample rate in terms of the bandwidth for the class of functions. The theorem also leads to a formula for perfectly reconstructing the original continuous-time function from the samples.
