steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
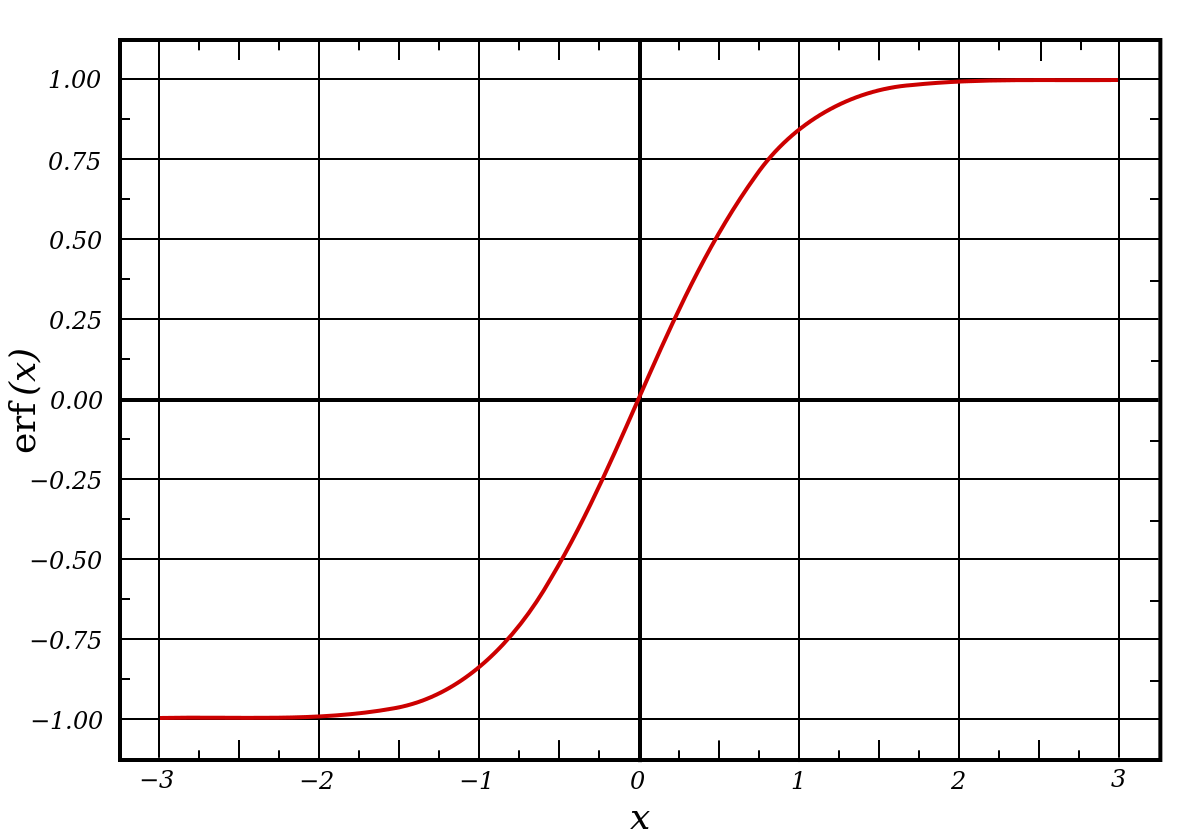
The error function and inverse error function.
Both important.
The error function is done by numerical integration. The inverse function by a series.
At small x values the precision is about 12 decimal places. It goes down as the magnitude of x increases.
The c coefficients for the inverse function could be precalculated and included as a table to speed up execution.
There is a series solution for the error function but have not tried it yet.
 en.wikipedia.org
en.wikipedia.org
I went around in circles trying to figure put why I was not getting the number of decimal places I expected. Turned out I had to explicitly make arrays a double. It looks e otherwise they ended up as floats.
Both important.
The error function is done by numerical integration. The inverse function by a series.
At small x values the precision is about 12 decimal places. It goes down as the magnitude of x increases.
The c coefficients for the inverse function could be precalculated and included as a table to speed up execution.
There is a series solution for the error function but have not tried it yet.

Error function - Wikipedia
I went around in circles trying to figure put why I was not getting the number of decimal places I expected. Turned out I had to explicitly make arrays a double. It looks e otherwise they ended up as floats.
Code:
import math as ma
import cmath as cm
import numpy as np
import array as ar
import matplotlib.pyplot as plt
#-------------------------------------------------------------
def plotxy(xlo,xhi,ylo,yhi,x,y,title,xlabel,ylabel):
# single y plot
font1 = {'family': 'arial',
'color': 'black',
'weight': 'heavy',
'size': 15,
}
[fig, p1] = plt.subplots(1)
p1.plot(x,y,linewidth=2.0,color="k")
p1.grid(color='k', linestyle='-', linewidth=1)
p1.grid(which='major', color='k',linestyle='-', linewidth=0.8)
p1.grid(which='minor', color='k', linestyle='-', linewidth=0.3)
p1.set_xlim(xlo,xhi)
p1.set_ylim(ylo,yhi)
p1.set_title(title, fontdict = font1)
p1.set_xlabel(xlabel, fontdict = font1)
p1.set_ylabel(ylabel, fontdict = font1)
p1.minorticks_on()
plt.show()
#-------------------------------------------------------------------------------
def coef():
nc = 100
c = nc*[0]
c[0] = 1
for k in range(nc):
for m in range(k):
c[k] += (c[m]*c[k-1-m])/((m+1)*(2*m + 1))
for k in range(10):
print(c[k])
#---------------------------------------------------------------------------
def erf(x):
# error function
# trapezoidal integration
if abs(x) == 0.0: return 0.0
sign = 1
if x < 0.0:sign = -1.
x = abs(x)
s = 0.
t = 0.
n = 500000
dt = x/n
for i in range(n):
y1 = ma.exp(-t*t)
t2 = t + dt
y2 = ma.exp(-t2*t2)
s += y1 + (y2-y1) *.5
t += dt
s *= dt*2./ma.sqrt(ma.pi)
return s * sign
#----------------------------------------------------------------------
def ierf(x):
# inverse error function
# adapted from wiki page on the error function
nc = 1000
c = ar.array('d',nc*[0])
c[0] = 1
for k in range(nc):
for m in range(k):
c[k] += (c[m]*c[k-1-m])/((m+1)*(2*m + 1))
einv = 0
q = ma.sqrt(ma.pi)*x/2.
for k in range(nc):
einv += ((c[k])/(2*k+1))*pow(q,(2*k+1))
return einv
#-----------------------------------------------------------------------
def norm_dist(n,y,u,sigma):
k = ma.sqrt(2)*sigma
for i in range(n):
# p>0, <1
p = 0
while(p == 0):
p = rn.random()
p = 2.*p-1.
y[i] = u + ierf(p)*k
#--------------------------------------------------------------------
n = 22
x = ar.array('d',n*[0])
y = ar.array('d',n*[0])
yi = ar.array('d',n*[0])
# testing ierf()
dx = .1
xsum = 0.123456789012345
for i in range(n):
x[i] = xsum
y[i] = erf(xsum)
yi[i] = ierf(y[i])
xsum += dx
for i in range(n):
print("%+.15f %.15f %+.15f" %(x[i],y[i],yi[i]))
n = 100
t = np.linspace(-2,2,n)
y = ar.array('d',n*[0])
x = ar.array('d',n*[0])
for i in range(n):
y[i] = y[i] = erf(t[i])
x[i] = ma.exp(-t[i]*t[i])
plotxy(min(t),max(t),min(y),max(y),t,y,"error function","","")
plotxy(min(t),max(t),min(x),max(x),t,x,"integrated function","","")