steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
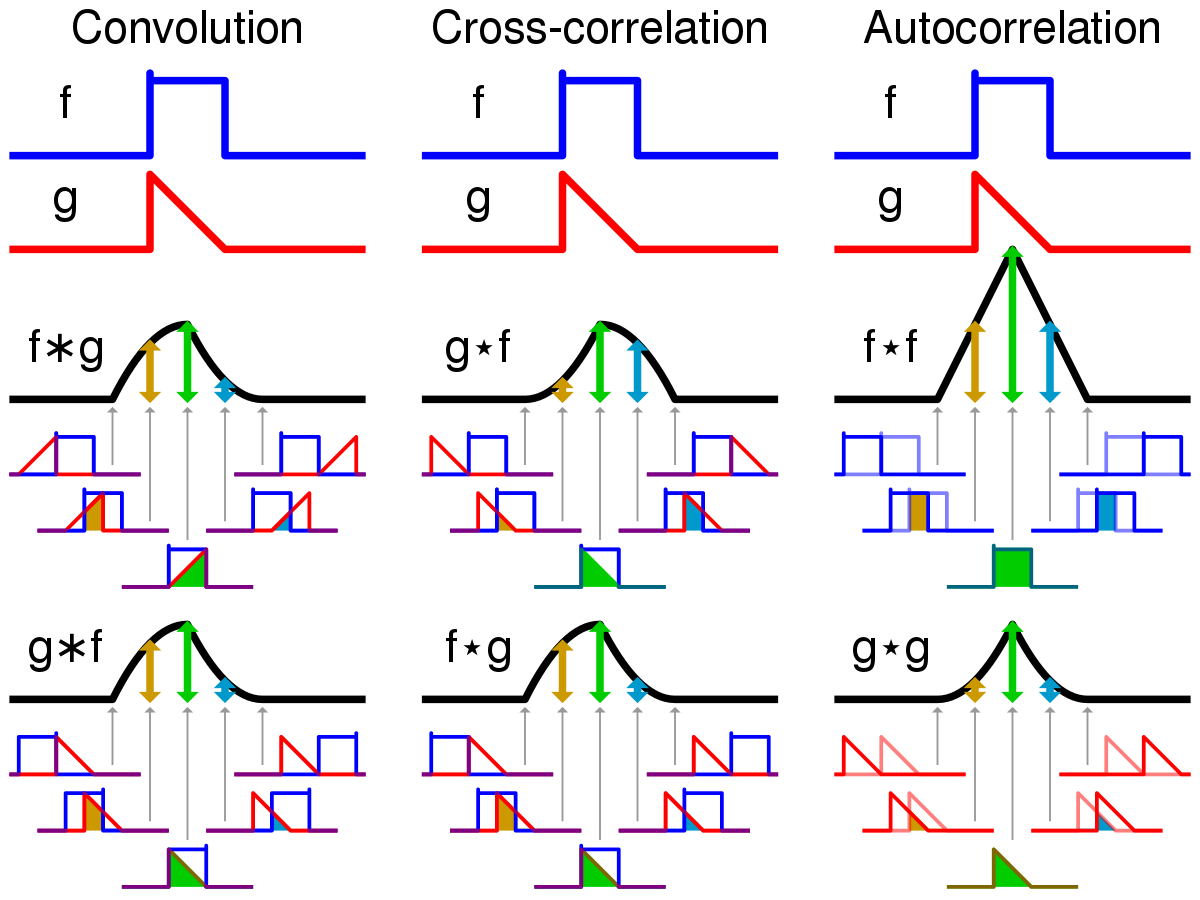
Tie and frequency domain convolution are fundamental methods in dynamic electoral circuits and dynamic mechanical systems.
Convolution to fid the output of a system for an input, Deconvolution is used to untangle components of a system response.
In tie domain convolution two functions in tine are multiplied as they pass by each other. There is an animation in the link.
The saying for frequency domain convolution is ‘convolution in the time domain is multiplication in the frequency domain’.
The output of the FFT is a complex frequency domain array. The FFT of two time domain signals are taken. The results multiplied, then the inverse FFT is taken.
Tine domain → FFT --> frequency domain --> inverse FFT --> time domain
The decaying exponential is the impulse response of a simple resistor capacitor low pass filter. Convolving the exponential impulse response with a pule results in the expected delayed response.
The impulse response is when you inject a short duration pulse into a system. Tapping a bell with a hammerer is an approximation to an impulse.
The impulse response of a 1st order differential equitation is a decaying exponential.
I stared to do it in Python but it got too troublesome.
There are numerous videos and sites on convolution. As is often true lengthy math reduces to simple implementations.
 en.wikipedia.org
en.wikipedia.org
Y1

Y2

Convolution 1st order lag

Convolution to fid the output of a system for an input, Deconvolution is used to untangle components of a system response.
In tie domain convolution two functions in tine are multiplied as they pass by each other. There is an animation in the link.
The saying for frequency domain convolution is ‘convolution in the time domain is multiplication in the frequency domain’.
The output of the FFT is a complex frequency domain array. The FFT of two time domain signals are taken. The results multiplied, then the inverse FFT is taken.
Tine domain → FFT --> frequency domain --> inverse FFT --> time domain
The decaying exponential is the impulse response of a simple resistor capacitor low pass filter. Convolving the exponential impulse response with a pule results in the expected delayed response.
The impulse response is when you inject a short duration pulse into a system. Tapping a bell with a hammerer is an approximation to an impulse.
The impulse response of a 1st order differential equitation is a decaying exponential.
I stared to do it in Python but it got too troublesome.
There are numerous videos and sites on convolution. As is often true lengthy math reduces to simple implementations.

Convolution - Wikipedia
Code:
//Sxilab
// time andd frequncy domain convolution
clear
clc
function plotxy(x,y,xlo,xhi,ylo,yhi)
scf()
a = gca()
plot(x,y,'k',"linewidth",2.5)
a.font_size = 4
a.font_color = -1
a.data_bounds = [xlo,xhi,ylo,yhi]
xgrid(1,4)
endfunction
disp("convolution")
n = 2^10 // power of
tau = .03
tmax = 1
dt = tmax/(n-1)
k = 1
// crete pulse and decaying exponentiall time domin signals
for i = 1:n
t(i) = i*dt
y1(i) = k*exp(-t(i)/tau)
y2(i) = 0
if(t(i) >= .2 && t(i) <= .6)
y2(i) = 1
end
end
// tie domain convolution
for i = 1:n
s = 0
for j =1:i
s = s +y2(j) *y1(i-j+1)
end
c(i) = s
end
plotxy(t,c,0,1,min(c),max(c))
// frequency dmoain convolution
y1fft = fft(y1)
y2fft = fft(y2)
for i = 1:n
c(i) = y1fft(i)*y2fft(i)
end
ci = real(ifft(c))
plotxy(t,ci,0,1,min(ci),max(ci))
plotxy(t,y1,0,1,0,2)
plotxy(t,y2,0,1,0,2)Y1

Y2

Convolution 1st order lag

Last edited:
