• Welcome to the new Internet Infidels Discussion Board, formerly Talk Freethought.

Discrete Fourier Trasform

S

steve_bank

Diabetic retinopathy and poor eyesight. Typos ...
Joined
Nov 9, 2017
Messages
13,779
Location
seattle
Basic Beliefs
secular-skeptic
The Discrete Fourier Transform

There is plenty of code on the met, but little of it are usable. I went through this exercise in the 80s while reading Brigam's book. The main reason I got my first computer ad learned C was to go through exercises like this. I heard it said the best way to learn something is to code it.

The actual transform occurs in one line, the summation of the Fourier series. The transform is in exponential form. The rest of code is to a,e the transform usable.

Ye FFT is essentially a correlation integral. The transform is blind. The meaning comes from the scale factors in this case electrical time and frequency.

At each frequency in the transform a the sine-cosine is broken into n bits, and each bit is coelrted to a pint in tine in the time record.

An important aspect is samplmg. The smapling theorm staes that yiu meed to sample at at leat at 2x the highest sampled frequency. In practice it is usually higher than that. I don't know what the current digital audio sampling frequency is for a 2okz bandwidth.

Another aspect of sampling is aliasing. If you run the transform at 10, 1010,2010 hz with a sampling frequency of 2000 hz the transform frequency will be 10 in all cases.

Higher sampling frequency also means lower noise. The abrupt steps in t sample record transform to noise. More samples means smaller changes from sample to sample. Quantization noise.

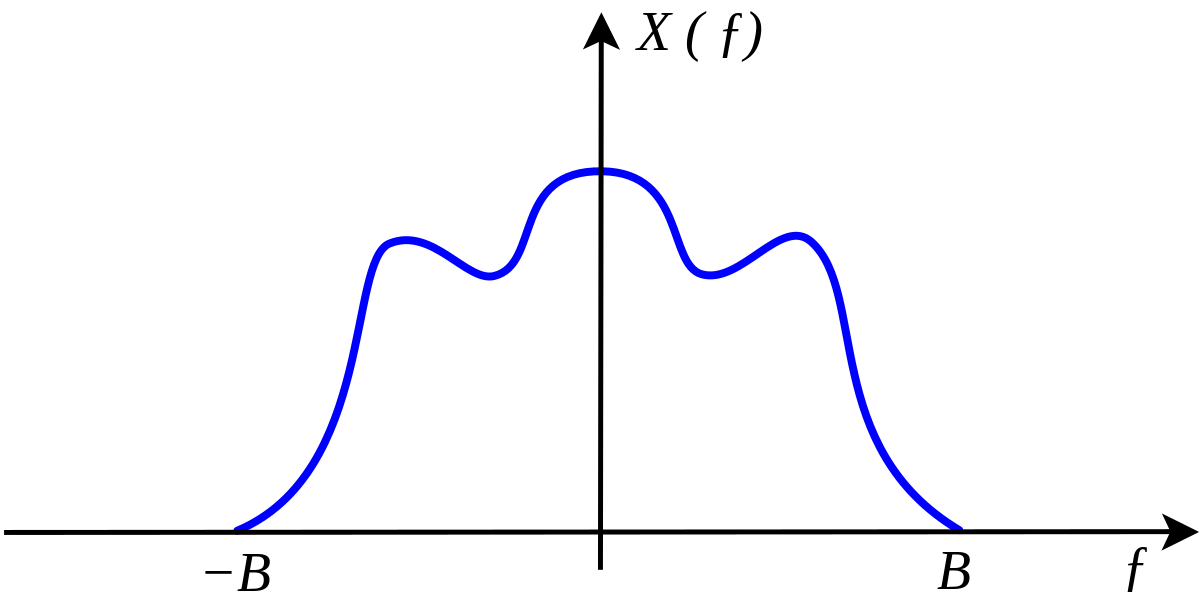
If the sample record at the ends are not exactly zero the abrupt change again transforms to noise. Window functions modify the ends of record. Windowing reduces amplitude accuracy in trade for better frequency resolution.

An n point transform generates 2 mirror spectrums centered at n/2. The transform only needs to run from zero to 1/n. Runs faster. The ergy is split between the two mirror spectrums, so the true amplitude of a line is 2x the transform output.

The inverse transform goes from a complex frequency spectrum back to a tome domain signal.

There is an uncertainty aspect to the Fourier Trasform.
Time resolution is dt = 1 /fs where dt is the sampleinterval and fs is the sampling frequency. Frequency resolution df = fs/n. As fs goes up increasing time resolution df goes down. For a d fixed n.

The DFT is suitable for some application, the Fast Fourier Transform is used for general applications. The FFT is an optimization of the DFT making use of redundant calculations. The Cooley Tukey paper is included.

Sclab script for plotting is included if you compile and run the code. Scilab has fubctis that read ausio files and calculates a frequency spectrum. You could build your own basic voice password recognition system. Scilab is free.

Things you can do with it.
A single pule of variable width, a single or sum of two sines, and amplitude modulation can bw creted.

Create two sines and see how close they can be and resolved while varying fs,n, and applying a window.

Look at a pulse transform as pulse width is made smaller and larger,

Force an alias.

A 2^12 transform is under a second on my machine. 2^14 10 seconds,2^16 2 minutes.

For the mathematically inclined some light reading.

Window Functions
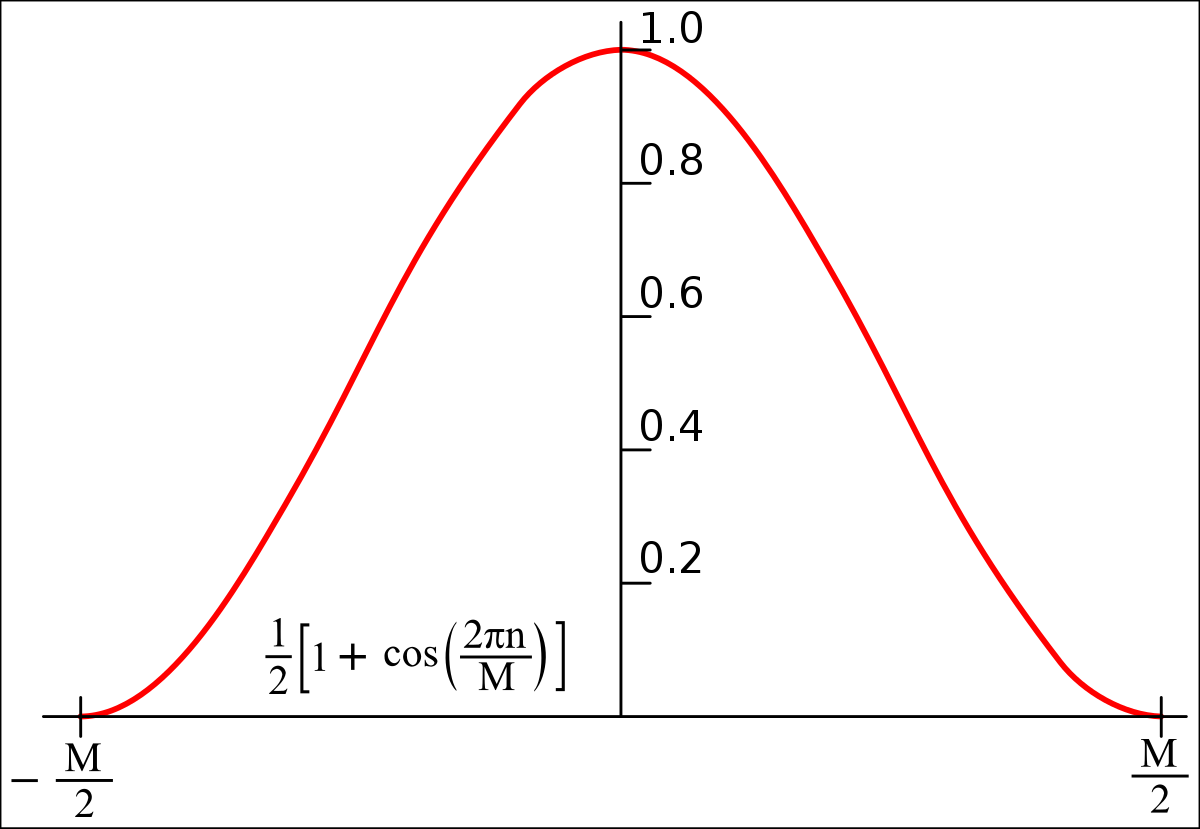
en.wikipedia.org

Window function - Wikipedia

en.wikipedia.org en.wikipedia.org

Tukey's and Cooley's paper

archive.org

BSTJ 37: 1. January 1958: The Measurement of Power Spectra from the Point of View of Communications Engineering - Part I. (Blackman, R.B.; Tukey, J.W.) : Free Download, Borrow, and Streaming : Internet Archive

Bell System Technical Journal, 37: 1. January 1958 pp 185-282. The Measurement of Power Spectra from the Point of View of Communications Engineering - Part I....
archive.org

Brigham

Fourier Uncertainty Principle

Sampling Theorem
en.wikipedia.org

Nyquist–Shannon sampling theorem - Wikipedia

en.wikipedia.org en.wikipedia.org
 
Code: 
#include "string.h"
#include <iostream>
#include <fstream>
#include "math.h"
#include "stdlib.h"
#include "stdio.h"
#include <complex>
#define _2PI 6.2831853071799586232
using namespace std;

typedef complex<double> compvar;
const double FWD = -1.;
const double INV = 1.;
const int NONE = 0;
const int HANN = 1;
const int TUKEY = 2;


int n = pow(2,12); //transform size 2^8,2^9,2^10...

double *yr = new double[n];
double *yinv = new double[n];
double *mag = new double[n];
double *ph = new double[n];
double *t = new double[n];
double *f = new double[n];
compvar *tfout = new compvar[n];

void save(int n,double *mag,double *ph,
         double *y, double *yinv,double *t, double *f) {
    int i;
    FILE *fptr;
    fptr = fopen("sig.txt","w");
    fprintf(fptr,"%d\n",n);
    for (i = 0; i < n; i++){
        fprintf(fptr,"%3.5f    %8.4f    %10.4f    %10.4f    %4.5f    %2.2f\n",
          t[i],f[i],y[i],yinv[i],mag[i],ph[i]);
    }//for
    fclose(fptr);
    cout << "SAVE DONE" << "\n";
}//save()

class DFT{
public:
    double *yinv, *yr; //real signal in and out
    compvar *tfout; // complex fprward trasform out
    int N = 2^10; //transform length
    double *mag,*ph; //transform magnitude and ohase
    double flag = FWD; //trasform type
    int wintype = NONE; //NONE, HANN, TUKEY
    double alpha = .2; //Tukey window paremeter 0 - 1

    void run(void) {

    if(flag == FWD)cout << "FORWARD " << "\n";
            else cout << "INVERSE" << "\n";
    compvar sum,W,C3;
    int freq, k;
    double C2;
    W = 0. + 1.i*flag * _2PI/double(N);
    C2 = 2. / double(N);

    for (freq = 0; freq < N/2; freq++) {
        C3 = W * double(freq); //complex frequency
        sum = 0. + 0.i;

        if(flag == FWD){
          for (k = 0; k < N; k++)sum += yr[k]*exp(C3*double(k));
          tfout[freq] = sum; //complex transform out
          if (freq == 0){
            //mag[0] is the average  value
            ph[freq] = 0;
            mag[freq] = real(sum)/double(N);
            }
            else{
             mag[freq] = C2*abs(sum);
             ph[freq] = (360./_2PI)*atan(imag(sum)/real(sum));
              }
          }//if fwd

        if(flag == INV){
          for (k = 0; k < N; k++)sum += tfout[k]*exp(C3*double(k));
          yinv[freq] = (C2*real(sum))-mag[0];//restore correct average value
          }//if inv

   }//for freq
   cout<<"TRANSFORM DONE"<<endl;
}//run()


void window(void){
    int i = 0;
    double w = 0.;
    switch(wintype){
        case NONE:
        cout<<"NO WINDOW"<<endl;
        break;
        case HANN:
        cout<<"HANN WINDOW"<<endl;
        for(i = 0; i <N;i++)
         yr[i] = yr[i]*.5*(1. - cos(_2PI*i/double(N - 1)) );
        break;
        case TUKEY:
        cout<<"TUKEY WINDOW"<<endl;
        for(i = 0;i<alpha*N/2;i++){
          w = .5*(1.- cos(_2PI*i/(alpha*double(N - 1))));
          yr[i] = w*yr[i];
          yr[N-1-i] = w*yr[N-1-i];
       }
        break;
        default: break;
    }//switch

}//window

};//class DFT

class SigGen{
public:

    double a1,a2,f1,f2,dc1,dc2,ph1,ph2;
    double *f,*t,fs,*y;
    double thi,tlo;
    int n;

    void make_pulse(void){
        // creates smgle non repetitive pulse
        cout<<"MAKE_PULSE"<<endl;
        int i = dc1;
        if(thi > t[n-1]) thi = t[n-1];
        if(tlo < 0.) tlo = 0;
        for(i = 0;i <n;i++){
            yr[i] = dc1;
            if(t[i] >= tlo && t[i] <= thi) yr[i] = a1 + dc1;
        }//for
        cout<<"MAKE_PULSE DONE"<<endl;
    }//make_pulse()

    void am(void){
    // creates amplitude modulation signal
    cout<<"AM"<<endl;
    int i;
    for(i=0;i<n;i++)yr[i] = (a1-a2*sin(_2PI*f2*t[i]))*sin(_2PI*f1*t[i]);
    }//am()

    void freq_time(void){
        //creates time and freqincy scaling
        cout<<"FREQ_TIME"<<endl;
        int i = 0;
        double fcount = 0,tcount = 0, df = fs/double(n),dt = 1./fs;
        for(i = 0;i < n; i++){
            t[i] = tcount;
            f[i] = fcount;
            tcount += dt;
            fcount += df;
        }//for
    //printf("fmax %f  fs %f  df %f dt %f  n %d\n", fmax,fs,df,dt,n);
    cout<<"FREQ_TIME DONE"<<endl;
}//freq_time()

    void make_sin(void){

        // sum of two sin waves
        cout<<"MAKE_SIN"<<endl;
        int i;
        double y1,y2;
        for( i = 0; i < n;i++){
            y1 = a1*sin(_2PI * f1 * t[i] +ph1) + dc1;
            y2 = a2*sin(_2PI * f2 * t[i] + ph2) + dc2;
            y[i] = y1 + y2;
        }//for
        cout<<"MAKE_SIN DONE"<<endl;
}//make_sin()

};//SigGen

int main()
{
    cout<<"N  "<<n<<endl;
    DFT dft;
    SigGen sg;

    sg.y = yr;
    sg.tlo = 1.;sg.thi = 1.05;
    sg.n = n; sg.fs = 2000.;
    sg.a1 = 50.;sg.f1 = 100.;sg.dc1 = 0.;sg.ph1 = 0.;
    sg.a2 = 0.;sg.f2 = 20.;sg.dc2 = 0.;sg.ph2 = 0.;
    sg.t = t; sg.f = f;
    sg.freq_time();
    sg.make_sin();
    //sg.make_pulse();
    //sg.am();

    dft.N = n;
    dft.yr = yr; dft.yinv = yinv;
    dft.mag = mag;dft.ph = ph;
    dft.tfout = tfout;
    dft.alpha = .4;
    dft.wintype = NONE;
    dft.window();
    dft.flag = FWD;
    dft.run();
    dft.flag = INV;
    dft.run();

    save(n,mag,ph,yr,yinv,t, f);

    cout << "DONE" << endl;
    return 0;
}
 
Code: 
 //y- t[i], f[i], y[i], yinv[i], mag[i] ,ph
clear
clc
path ="xxx"
s = path + "sig.txt"
mclose("all")
[f1,err] = mopen(s,"rt")
if(err < 0)then disp("file open error   ",err);end;
N = mfscanf(1,f1," %d")
y = mfscanf(N,f1," %f  %f  %f %f  %f %f ")
mclose("all")
//mprintf("%f  %f  %f  %f  %f  %f\n",y)

w1 = scf(1)
clf(w1)
subplot(2,2,1)
plot2d(y([1:N/2],1),y([1:N/2],3))
title"SIGNAL"
xgrid
subplot(2,2,3)
plot2d(y([1:N/2],1),y([1:N/2],4))
title("INV SIGNAL ")
xgrid
subplot(2,2,2)
plot2d3(y([1:N/2],2),y([1:N/2],5))
title("MAG ")
xgrid
subplot(2,2,4)
plot2d(y([1:N/2],2),y([1:N/2],6))
title("PHASE ")
xgrid
 
Some of the mathematics is interesting.

The discrete Fourier transform from n points of x to y:

\( \displaystyle{ y(a) = \sum_{b=0}^{n-1} e^{2\pi i a b / n} x(b) } \)

with inverse:

\( \displaystyle{ x(a) = \frac{1}{n} \sum_{b=0}^{n-1} e^{- 2\pi i a b / n} y(b) } \)

for a = 0 to (n-1).

At first sight, this requires a run time of O(n2). But some number theory comes to the rescue. One can factor a number into a product of primes, and one can decompose the DFT into DFT's involving those prime numbers. So one gets, for

n = product of primes p

a run time of O(n * sum of p)

If n is a power of 2, this reduces to O(n * log n)
 
You must log in or register to reply here.
Back
Top Bottom