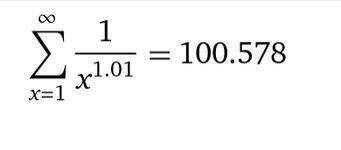-
Features
-
Friends of IIDBFriends Recovering from Religion United Coalition of Reason Infidel Guy
Forums Council of Ex-Muslims Rational Skepticism
Social Networks Internet Infidels Facebook Page IIDB Facebook Group
IIDB Archives FRDB Archive Secular Café Archive
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Infinite Sum
- Thread starter SLD
- Start date
Jarhyn
Wizard
- Joined
- Mar 29, 2010
- Messages
- 14,706
- Gender
- Androgyne; they/them
- Basic Beliefs
- Natural Philosophy, Game Theoretic Ethicist
Eventually when adding smaller and smaller numbers which all operations of this equation must, the numbers you add become too small to throw it off of convergence.Take the sum of x from 1 to infinity of 1/x^n, can anyone prove that it always converges for all n > 1? It does not for n=1. Obviously it converges for n=2 and greater. By experiment it also converges for n=1.01. But will it converge for some n infinitesimally close to 1? And a proof of such.
View attachment 40116
Any shrinkage in the process will cause later iterations to lose their significance over time, and when that significance is lost, convergence begins to happen.
It happens because for any constant nonzero amount of "loss of significance over time", eventually significance will move towards zero, so at "infinity", significance of additional iterations is going to be infinitely small.
The only way to prevent the loss of significance of interactions would be to shift the exponent over time.
The system of how much significance is lost, as N increases, asymptotically approaches 0.
It might be better to look at your equation from the standpoint of 1/(n^(x+1)), and map the asymptotes of the graph of this system of infinite sums.
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
I'd have to look up how to test a series for convergence. Can't do it off the top of my head.Take the sum of x from 1 to infinity of 1/x^n, can anyone prove that it always converges for all n > 1? It does not for n=1. Obviously it converges for n=2 and greater. By experiment it also converges for n=1.01. But will it converge for some n infinitesimally close to 1? And a proof of such.
View attachment 40116
But limit as n > 1 from +inf (x^n) = x.
So in the limit it is sum 1/x 1 to inf. As x gets large the terms asymptotically go to zero so I'd think it converge but maybe not.
You can look up on the net how to test a series for convergence.
lpetrich
Contributor
Proof of convergence for
\( \displaystyle{ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} } \)
for Re(s) > 1:
I will use that definition and not analytical continuations of that definition for Re(s) <= 1.
First off, ζ(s) > 0 for all s, supplying a lower bound. So we must look for an upper bound. Since this series diverges for Re(s) <= 0, we look at Re(s) > 0. Finding a lower bound for each n thus gives an upper bound for the series. We can also find a lower bound by finding an upper bound for each n, something that will improve our convergence estimate.
Lower bound for each n: (1) >= 1, (2, 3) >= 2, (4, 5, 6, 7) >= 4, ... giving 2k of n = 2k
Upper bound for each n: (1) <= 1, (2) <= 2, (3, 4) <= 4, (5, 6, 7, 8) <= 8, ... giving 1, then 2k of each n = 2k+1
Thus,
\( \displaystyle{ 1 + \sum_{k=0}^\infty \frac{2^k}{2^{s(k+1)}} < \zeta(s) < \sum_{k=0}^\infty \frac{2^k}{2^{sk}} } \)
Both bounds are geometric series:
\( \displaystyle{ 1 + \sum_{k=0}^\infty \frac{2^k}{2^{s(k+1)}} < \zeta(s) < \sum_{k=0}^\infty \frac{2^k}{2^{sk}} } \)
reducing to
\( \displaystyle{ 1 + 2^{-s} \sum_{k=0}^\infty 2^{-(s-1)k} < \zeta(s) < \sum_{k=0}^\infty 2^{-(s-1)k}} \)
This means that the series form of ζ(s) converges for Re(s) > 1 and diverges for Re(s) <= 1.
There's a lot more at Riemann zeta function
Riemann zeta function
\( \displaystyle{ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} } \)
for Re(s) > 1:
I will use that definition and not analytical continuations of that definition for Re(s) <= 1.
First off, ζ(s) > 0 for all s, supplying a lower bound. So we must look for an upper bound. Since this series diverges for Re(s) <= 0, we look at Re(s) > 0. Finding a lower bound for each n thus gives an upper bound for the series. We can also find a lower bound by finding an upper bound for each n, something that will improve our convergence estimate.
Lower bound for each n: (1) >= 1, (2, 3) >= 2, (4, 5, 6, 7) >= 4, ... giving 2k of n = 2k
Upper bound for each n: (1) <= 1, (2) <= 2, (3, 4) <= 4, (5, 6, 7, 8) <= 8, ... giving 1, then 2k of each n = 2k+1
Thus,
\( \displaystyle{ 1 + \sum_{k=0}^\infty \frac{2^k}{2^{s(k+1)}} < \zeta(s) < \sum_{k=0}^\infty \frac{2^k}{2^{sk}} } \)
Both bounds are geometric series:
\( \displaystyle{ 1 + \sum_{k=0}^\infty \frac{2^k}{2^{s(k+1)}} < \zeta(s) < \sum_{k=0}^\infty \frac{2^k}{2^{sk}} } \)
reducing to
\( \displaystyle{ 1 + 2^{-s} \sum_{k=0}^\infty 2^{-(s-1)k} < \zeta(s) < \sum_{k=0}^\infty 2^{-(s-1)k}} \)
This means that the series form of ζ(s) converges for Re(s) > 1 and diverges for Re(s) <= 1.
There's a lot more at
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
Ipetrich,
Are you saying 1/(x^1) does not converge?
Are you saying 1/(x^1) does not converge?
lpetrich
Contributor
I'm guessing that you meanIpetrich,
Are you saying 1/(x^1) does not converge?
\( \displaystyle{ \zeta(1) = \sum_{n=1}^\infty \frac{1}{n} } \)
That series does not converge. In fact, partial sums have a limit:
\( \displaystyle{ \sum_{n=1}^\N \frac{1}{n} = \log N + \gamma + O(1/N) } \)
where γ = 0.577... is the Euler-Mascheroni constant.
lpetrich
Contributor
The zeta function, as it's called, can be extended beyond Re(s) > 1 by analytic continuation.
It can be expressed as an integral:
\( \displaystyle{ \zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{x^{s-1}}{e^x - 1} dx } \)
One can extend convergence to Re(s) > 0 with some rearrangement:
\( \displaystyle{ \zeta(s) = \frac{1}{1-2^{1-s}} \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^s} = \frac{1}{1-2^{1-s}} \frac{1}{\Gamma(s)} \int_0^\infty \frac{x^{s-1}}{e^x + 1} dx } \)
where Γ(x) is a generalization of the factorial function: Γ(x) = (x-1)! for positive integer x.
For s near 1,
\( \displaystyle{ \zeta(s) = \frac{1}{s-1} + \gamma + \dots } \)
It can be expressed as an integral:
\( \displaystyle{ \zeta(s) = \frac{1}{\Gamma(s)} \int_0^\infty \frac{x^{s-1}}{e^x - 1} dx } \)
One can extend convergence to Re(s) > 0 with some rearrangement:
\( \displaystyle{ \zeta(s) = \frac{1}{1-2^{1-s}} \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^s} = \frac{1}{1-2^{1-s}} \frac{1}{\Gamma(s)} \int_0^\infty \frac{x^{s-1}}{e^x + 1} dx } \)
where Γ(x) is a generalization of the factorial function: Γ(x) = (x-1)! for positive integer x.
For s near 1,
\( \displaystyle{ \zeta(s) = \frac{1}{s-1} + \gamma + \dots } \)
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
I guess I did not fully comprehend the meaning of convergence and divergence.
I took convergence to mean asymptotically approaching a value as the series goes to infinity. I may be confusing limits with convergence and divergence.
From this link 1/x flattens out, but the area goes to infinity, diverges.
Learn something new every day....
I took convergence to mean asymptotically approaching a value as the series goes to infinity. I may be confusing limits with convergence and divergence.
From this link 1/x flattens out, but the area goes to infinity, diverges.
Learn something new every day....
lpetrich
Contributor
One can define convergence of a sequence without reference to the limit that a sequence converges to. A convergent sequence defined in this way is a "Cauchy sequence", named after early 19th cy. French mathematician Augustin-Louis Cauchy.
First, when a series has a limit. Consider a sequence a(n) for n = 1, 2, 3, ... with limit a(lim). Then for every e > 0, there is some N such that |a(n) - a(lim)| < e for all n > N.
Now the Cauchy definition. For every e > 0, there is some N such that |a(n) - a(m)| < e for all n, m > N.
The nice thing about the Cauchy definition is that one defined convergence without reference to the sequence limit, because the limit may not be a member of some set that the sequence members are defined in.
Consider these sequences of positive numbers: 1, 1/2, 1/3, 1/4, 1/5, ... and 1, 1/2, 1/4, 1/8, 1/16, ...
They both have limit 0, and 0 is not a positive number.
Real numbers can be defined in terms of rational numbers as the limits of all Cauchy sequences of rational numbers. Real numbers are also the limits of all Cauchy sequences of real numbers, making them Cauchy-closed.
First, when a series has a limit. Consider a sequence a(n) for n = 1, 2, 3, ... with limit a(lim). Then for every e > 0, there is some N such that |a(n) - a(lim)| < e for all n > N.
Now the Cauchy definition. For every e > 0, there is some N such that |a(n) - a(m)| < e for all n, m > N.
The nice thing about the Cauchy definition is that one defined convergence without reference to the sequence limit, because the limit may not be a member of some set that the sequence members are defined in.
Consider these sequences of positive numbers: 1, 1/2, 1/3, 1/4, 1/5, ... and 1, 1/2, 1/4, 1/8, 1/16, ...
They both have limit 0, and 0 is not a positive number.
Real numbers can be defined in terms of rational numbers as the limits of all Cauchy sequences of rational numbers. Real numbers are also the limits of all Cauchy sequences of real numbers, making them Cauchy-closed.
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
Thanks.
SLD
Contributor
That’s right. If you integrate 1/x from 1 to infinity You get infinity. If some one said for you to paint the wall of 1/x from 1 to infinity, you might say it can’t be done. But you’d be wrong. What is the volume of the bounded trumpet formed by rotating 1/x around the x axis? The answer is pi! Try it. It’s a simple integration. So all you have to do is create a circular barrier around the function and fill it with pi units of paint and voila, you’ve painted an infinite area wall!I guess I did not fully comprehend the meaning of convergence and divergence.
I took convergence to mean asymptotically approaching a value as the series goes to infinity. I may be confusing limits with convergence and divergence.
From this link 1/x flattens out, but the area goes to infinity, diverges.
Learn something new every day....
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
That’s right. If you integrate 1/x from 1 to infinity You get infinity. If some one said for you to paint the wall of 1/x from 1 to infinity, you might say it can’t be done. But you’d be wrong. What is the volume of the bounded trumpet formed by rotating 1/x around the x axis? The answer is pi! Try it. It’s a simple integration. So all you have to do is create a circular barrier around the function and fill it with pi units of paint and voila,I guess I did not fully comprehend the meaning of convergence and divergence.
I took convergence to mean asymptotically approaching a value as the series goes to infinity. I may be confusing limits with convergence and divergence.
From this link 1/x flattens out, but the area goes to infinity, diverges.
Learn something new every day....
I think I get it now
Sonids le you knew the answer before you asked the question.
SLD
Contributor
Well it seemed intuitively obvious, but I didn’t know what the proof was. Just experimentally it seems to approach infinity as n goes to 1. I knew 1 didn’t converge. The series gets infinitesimally closer to 1 the higher the number. But all even n take the from of pi^n/(natural number).That’s right. If you integrate 1/x from 1 to infinity You get infinity. If some one said for you to paint the wall of 1/x from 1 to infinity, you might say it can’t be done. But you’d be wrong. What is the volume of the bounded trumpet formed by rotating 1/x around the x axis? The answer is pi! Try it. It’s a simple integration. So all you have to do is create a circular barrier around the function and fill it with pi units of paint and voila,I guess I did not fully comprehend the meaning of convergence and divergence.
I took convergence to mean asymptotically approaching a value as the series goes to infinity. I may be confusing limits with convergence and divergence.
From this link 1/x flattens out, but the area goes to infinity, diverges.
Learn something new every day....
I think I get it now
Sonids le you knew the answer before you asked the question.
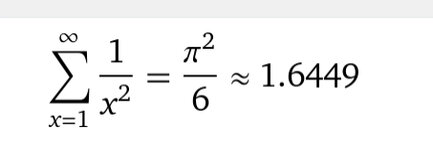
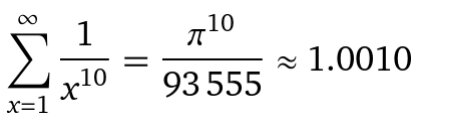

But odd numbers don’t show such a relationship.
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
When I was confronted by a work related problem It was more expedient to just simulate it.
Artemus
Veteran Member
Mathematically yes, but the engineering side in me is screaming "Gabriel's horn becomes narrower than a paint molecule's maximum dimension so you cannot fill it with paint."That’s right. If you integrate 1/x from 1 to infinity You get infinity. If some one said for you to paint the wall of 1/x from 1 to infinity, you might say it can’t be done. But you’d be wrong. What is the volume of the bounded trumpet formed by rotating 1/x around the x axis? The answer is pi! Try it. It’s a simple integration. So all you have to do is create a circular barrier around the function and fill it with pi units of paint and voila, you’ve painted an infinite area wall!
Jarhyn
Wizard
- Joined
- Mar 29, 2010
- Messages
- 14,706
- Gender
- Androgyne; they/them
- Basic Beliefs
- Natural Philosophy, Game Theoretic Ethicist
Maybe that's why it rings so loudly, on account of the molecule being compressed infinitely.Mathematically yes, but the engineering side in me is screaming "Gabriel's horn becomes narrower than a paint molecule's maximum dimension so you cannot fill it with paint."That’s right. If you integrate 1/x from 1 to infinity You get infinity. If some one said for you to paint the wall of 1/x from 1 to infinity, you might say it can’t be done. But you’d be wrong. What is the volume of the bounded trumpet formed by rotating 1/x around the x axis? The answer is pi! Try it. It’s a simple integration. So all you have to do is create a circular barrier around the function and fill it with pi units of paint and voila, you’ve painted an infinite area wall!
Gabriel as infinite blowhard?
SLD
Contributor
F$&#$king engineers. You have ruined mathematics!Mathematically yes, but the engineering side in me is screaming "Gabriel's horn becomes narrower than a paint molecule's maximum dimension so you cannot fill it with paint."That’s right. If you integrate 1/x from 1 to infinity You get infinity. If some one said for you to paint the wall of 1/x from 1 to infinity, you might say it can’t be done. But you’d be wrong. What is the volume of the bounded trumpet formed by rotating 1/x around the x axis? The answer is pi! Try it. It’s a simple integration. So all you have to do is create a circular barrier around the function and fill it with pi units of paint and voila, you’ve painted an infinite area wall!
lpetrich
Contributor
SLD posted on values for even powers. In general,
\( \displaystyle{ \zeta(2n) = \frac{ (-1)^{n+1} B_{2n} (2\pi)^{2n} }{ 2 (2n)! } } \)
where B(2n) is a "Bernoulli number", with this generating function:
\( \displaystyle{ \frac{t}{e^t - 1} = \sum_{n=0}^\infty \frac{B_n t^n}{n!} } \)
For all nonnegative integers n, B(n) is a rational number. For all odd n > 1, B(n) = 0. There are two conventions for the value of B(1): -1/2 and +1/2, and I've used the first one.
From the generating function, one can derive a sum formula,
\( \displaystyle{ \sum_{k=0}^n \binom{n+1}{k} B_k = \delta_{n,0} } \)
giving recurrence
\( \displaystyle{ B_n = \delta_{n,0} - \sum_{k=0}^{n-1} \binom{n}{k} \frac{B_k}{n-k+1} } \)
Bernoulli numbers are all rational numbers, and the zeta function for an even positive arg is (some rational number) * (pi)^(arg)
\( \displaystyle{ \zeta(2n) = \frac{ (-1)^{n+1} B_{2n} (2\pi)^{2n} }{ 2 (2n)! } } \)
where B(2n) is a "Bernoulli number", with this generating function:
\( \displaystyle{ \frac{t}{e^t - 1} = \sum_{n=0}^\infty \frac{B_n t^n}{n!} } \)
For all nonnegative integers n, B(n) is a rational number. For all odd n > 1, B(n) = 0. There are two conventions for the value of B(1): -1/2 and +1/2, and I've used the first one.
From the generating function, one can derive a sum formula,
\( \displaystyle{ \sum_{k=0}^n \binom{n+1}{k} B_k = \delta_{n,0} } \)
giving recurrence
\( \displaystyle{ B_n = \delta_{n,0} - \sum_{k=0}^{n-1} \binom{n}{k} \frac{B_k}{n-k+1} } \)
Bernoulli numbers are all rational numbers, and the zeta function for an even positive arg is (some rational number) * (pi)^(arg)
lpetrich
Contributor
For n > 1, the denominators of B(2n) all divide 2*(2n+1)!! where (2n+1)!! = 1*3*5*...*(2n+1).
Relatives of the Riemann zeta function
Riemann zeta function
\( \displaystyle{ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} } \)
 Dirichlet eta function
Dirichlet eta function
\( \displaystyle{ \eta(s) = \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^s} = (1 - 2^{1-s}) \zeta(s) } \)
Dirichlet lambda function - Lambda function
Lambda function
\( \displaystyle{ \lambda(s) = \sum_{n=1}^\infty \frac{1}{(2n+1)^s} = (1 - 2^{-s}) \zeta(s) } \)
 Dirichlet beta function
Dirichlet beta function
\( \displaystyle{ \beta(s) = \sum_{n=1}^\infty \frac{(-1)^{n+1}}{(2n+1)^s} } \)
I first learned about these functions long ago, from Abramowitz and Stegun: Handbook of Mathematical Functions (scanned print version)
[Edited as per request]
Relatives of the
\( \displaystyle{ \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} } \)
\( \displaystyle{ \eta(s) = \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n^s} = (1 - 2^{1-s}) \zeta(s) } \)
Dirichlet lambda function -
\( \displaystyle{ \lambda(s) = \sum_{n=1}^\infty \frac{1}{(2n+1)^s} = (1 - 2^{-s}) \zeta(s) } \)
\( \displaystyle{ \beta(s) = \sum_{n=1}^\infty \frac{(-1)^{n+1}}{(2n+1)^s} } \)
I first learned about these functions long ago, from Abramowitz and Stegun: Handbook of Mathematical Functions (scanned print version)
[Edited as per request]
Last edited by a moderator:
steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
Necessity is the mother of invention.
Mathematics came about as an aid to engineering.
Probability theory arose as an aid to gain an advantage at gambling.
Mathematics came about as an aid to engineering.
Probability theory arose as an aid to gain an advantage at gambling.