steve_bank
Diabetic retinopathy and poor eyesight. Typos ...
Doodling to ward off brain fog.
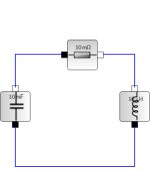
An example of energy and conservation, a parallel electrical circuit, a resonator. The electrical equivalent to a swinging pendulum.
It numericaly solves a second order differntial equation. In physical systems 2nd order infers two forms of energy storage. In this case the magnetic field of an inductor and electric field of a capacitor.
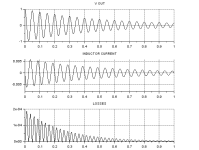
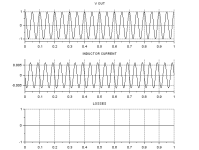
The energy shell game, what and where is it?Is energy a fluid running through wires? Without losses the enrgy goes back and forth between the inductr and capacitomathemetocally forever. When the capacitor energy is max the inductor energy is zero and vice versa.
With losses the system energy decreases exponential. The initial energy is 25 micro Joules. At 100 seconds the restrictive loss is almost exactly the same. At any point in time enrgy must always add up algebraically.
I = current
C capacirance
L inductance
t time
E energy
Capacitor
i = C*dv/dt) --> dv = (i*dt)/C. For a constant current dv is linear with time.
Inductor
v = L*(di/dt) → di = (v*dt)/L. For a constant voltage across an inductor current changes linearly.
Capacitors and inductors are duals.
Energy Joules
Ec = 0.5*v^2*C El = 0.5*iL^2*L
The solution is Euler’s Method. Piecewise linear approximation using differentials assuming linear changes during a simulation time step dt.
Power in a resistor watts W = i^2*r. 1W = 1J/second. E = t*W, total energy in Joules over a time period.
The resonant frequency is f = 1/(2*pi*√(L*C)). Civen a capacitor inductor is calculated.
Resonance is a general principle. It can be electrical, electromagnetic, mechanical, optical, or quantum. A system like a building structure can have multiple resonances. The Eigenvalues and Eigenvectors of the system equations.
//LC oscillator
// resonant frequency = 1/(2*pi*sqrt(LC))
// Euler's method
clear
function [rms_dc] = rms(x)
[n,m] = size(x)
s = 0
for i = 1:n s = s + x(i);end;
dc_avg = s/n
s = 0
for i = 1:n s = s + (x(i) - dc_avg)^2;end;
rms_ac = sqrt(s/n)
rms_dc = sqrt(rms_ac^2 + dc_avg ^2)
endfunction
fr = 20. // Osscilator Fequency Hertz
C = 50e-6 // farads
L = 1/(C*((2*%pi*fr)^2)) //henries
R = 5 //ohms
mrintf("L %f C %f R %f\n",L,C,R)
tmax = 1. // simulation time
dt = 50e-6 // solution tme step
t = [0:dt:tmax]' // time x axis plot array
Nsig= length(t) // record length
// Initial conditions
vc =1. // initial capacitor voltage
il = 0. // start with zero current in the inductor
ELi = 0.5 *L*(il^2)
ECi = .5*C* (vc^2) //initial system energy in capacitor
pwr_r = 0.
p = ECi
psum = 0
for i = 1:Nsig
Vo(i) = vc // circuit output
iL(i) = il
pwr_r = pwr_r + ((il^2)*R)
pR(i) = (il*il )*R
pC(i) = .5 * C*(vc^2) // instantaeous cap ind energy
pL(i) = .5 *L*(il^2)
psum = psum + pR(i)
pd(i) =((pL(i) + pC(i))/ECi) * 100. //%energy loss vs time
Vr(i) = R*il
di =( vc+ R*il)*(dt/L) // calculate next inductor current based on last capacitor voltage
il = il - di
dv = il*(dt/C) // calculate next capaitor voltage bdsed on last inductor current
vc = vc + dv
end//i
[rmsr] = rms(pR)
[irms] = rms(iL)
prms = (irms^2) * R * tmax // resistor losses
mprintf("I RMS %.10f P RMS %e\n",irms,prms)
mprintf("IND ENERGY %f CAP ENERGY %e\n",ELi,ECi)
//mprintf("R POWER RMS %.10f DC AVG %.10f SUM %.10f\n",rmsr,dcr,sumr)
mprintf("psum %f\n",psum)
An example of energy and conservation, a parallel electrical circuit, a resonator. The electrical equivalent to a swinging pendulum.
It numericaly solves a second order differntial equation. In physical systems 2nd order infers two forms of energy storage. In this case the magnetic field of an inductor and electric field of a capacitor.
The energy shell game, what and where is it?Is energy a fluid running through wires? Without losses the enrgy goes back and forth between the inductr and capacitomathemetocally forever. When the capacitor energy is max the inductor energy is zero and vice versa.
With losses the system energy decreases exponential. The initial energy is 25 micro Joules. At 100 seconds the restrictive loss is almost exactly the same. At any point in time enrgy must always add up algebraically.
I = current
C capacirance
L inductance
t time
E energy
Capacitor
i = C*dv/dt) --> dv = (i*dt)/C. For a constant current dv is linear with time.
Inductor
v = L*(di/dt) → di = (v*dt)/L. For a constant voltage across an inductor current changes linearly.
Capacitors and inductors are duals.
Energy Joules
Ec = 0.5*v^2*C El = 0.5*iL^2*L
The solution is Euler’s Method. Piecewise linear approximation using differentials assuming linear changes during a simulation time step dt.
Power in a resistor watts W = i^2*r. 1W = 1J/second. E = t*W, total energy in Joules over a time period.
The resonant frequency is f = 1/(2*pi*√(L*C)). Civen a capacitor inductor is calculated.
Resonance is a general principle. It can be electrical, electromagnetic, mechanical, optical, or quantum. A system like a building structure can have multiple resonances. The Eigenvalues and Eigenvectors of the system equations.
//LC oscillator
// resonant frequency = 1/(2*pi*sqrt(LC))
// Euler's method
clear
function [rms_dc] = rms(x)
[n,m] = size(x)
s = 0
for i = 1:n s = s + x(i);end;
dc_avg = s/n
s = 0
for i = 1:n s = s + (x(i) - dc_avg)^2;end;
rms_ac = sqrt(s/n)
rms_dc = sqrt(rms_ac^2 + dc_avg ^2)
endfunction
fr = 20. // Osscilator Fequency Hertz
C = 50e-6 // farads
L = 1/(C*((2*%pi*fr)^2)) //henries
R = 5 //ohms
mrintf("L %f C %f R %f\n",L,C,R)
tmax = 1. // simulation time
dt = 50e-6 // solution tme step
t = [0:dt:tmax]' // time x axis plot array
Nsig= length(t) // record length
// Initial conditions
vc =1. // initial capacitor voltage
il = 0. // start with zero current in the inductor
ELi = 0.5 *L*(il^2)
ECi = .5*C* (vc^2) //initial system energy in capacitor
pwr_r = 0.
p = ECi
psum = 0
for i = 1:Nsig
Vo(i) = vc // circuit output
iL(i) = il
pwr_r = pwr_r + ((il^2)*R)
pR(i) = (il*il )*R
pC(i) = .5 * C*(vc^2) // instantaeous cap ind energy
pL(i) = .5 *L*(il^2)
psum = psum + pR(i)
pd(i) =((pL(i) + pC(i))/ECi) * 100. //%energy loss vs time
Vr(i) = R*il
di =( vc+ R*il)*(dt/L) // calculate next inductor current based on last capacitor voltage
il = il - di
dv = il*(dt/C) // calculate next capaitor voltage bdsed on last inductor current
vc = vc + dv
end//i
[rmsr] = rms(pR)
[irms] = rms(iL)
prms = (irms^2) * R * tmax // resistor losses
mprintf("I RMS %.10f P RMS %e\n",irms,prms)
mprintf("IND ENERGY %f CAP ENERGY %e\n",ELi,ECi)
//mprintf("R POWER RMS %.10f DC AVG %.10f SUM %.10f\n",rmsr,dcr,sumr)
mprintf("psum %f\n",psum)