Jarhyn
Wizard
- Joined
- Mar 29, 2010
- Messages
- 14,734
- Gender
- Androgyne; they/them
- Basic Beliefs
- Natural Philosophy, Game Theoretic Ethicist
So, recently, I've been playing with analytical tools to do some dumb shit.
Willans formulae are functions that use brute force to check for primality, by taking some product and all of its products.
Currently, I have been playing with a constructable wave form as follows:
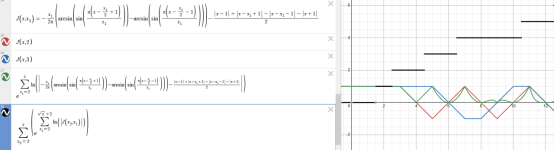
\(p\left(x,x_{1},x_{2}\right)\ =\tanh\left(-k\left(x-\left(2x_{1}\right)\left(x_{2}+2\right)\right)\right)-\tanh\left(-k\left(x-\left(2x_{1}+1\right)\left(x_{2}+2\right)\right)\right)\)
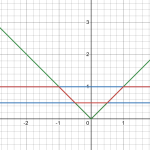
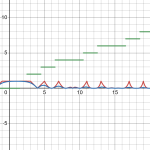
The purple is this:
\(p\left(x,0,0\right)\)
The green is this:
\(\left(1+\sum_{x_{1}=-s}^{s}p\left(x,x_{1},0\right)-p\left(x,0,0\right)\right)\)
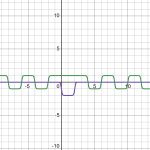
As can be seen, This function can be provoked to have zeros at places.
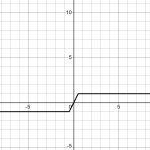
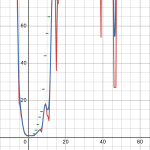
Recently, I also discovered THIS gem, which can be provoked to produce an even more exact structure:
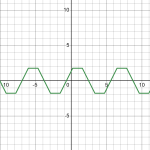
\(k\arcsin\left(\sin\left(x\right)\right)+k\arcsin\left(\sin\left(x+v\right)\right)\)
As can be seen in the following graph, the resulting wave is trapezoidal. at sufficiently high K, with v close enough to but less than pi the system becomes square, however using this to construct a willans/eratosthenes prime counter requires being able to take a bite out of it to make the product.
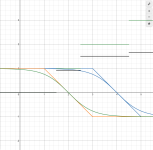
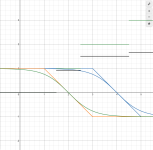
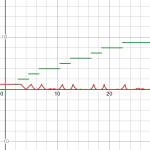
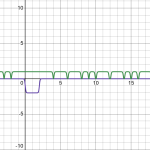
unfortunately, I've been having a hard time finding a single sum that represents a single "bite" out of such a trapezoidal system:
Is there even some function that continuously defines a line with a single trapezoid out of it? I think it would have to be the sum of two functions that define a single "zag" of a flat line the way the tanh sum does a "steplike shape", but I don't know any way to precisely define just one. It would dramatically speed up the productization time, and would allow an error-free infinite sum.
This connects to Willans methods in the following way:
\(\prod_{n=0}^{s}\left(1+\sum_{x_{1}=-s}^{s}p\left(x,x_{1},n\right)-p\left(x,0,n\right)\right)^{2}\)
\(\sum_{n_{2}=2}^{x}\prod_{n=0}^{s}\left(1+\sum_{x_{1}=-s}^{s}p\left(n_{2},x_{1},n\right)-p\left(n_{2},0,n\right)\right)^{2}\)
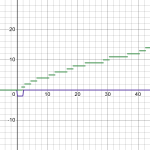
Such functions, when taken a bite out of them, represent "is divisible by" as a statement by their zeroes. By squaring such "bitten" wave functions, you can then productize them, representing "is divisible by any prior number".
The trapezoidal function seems the best fit for this, since it doesn't have error past the "shoulder" and while the productization is still expensive, this allows placing the flats so that the shoulders can't interfere with zero-ness of non-prime values between them nor the one-ness at primes. I suspect the trapezoidal function will require high values of K at arbitrarily high values of x, and arbitrarily precise measurements of pi, however, to keep the "shoulders" of higher "mutiple waves" from intruding, and that's assuming there's a function I can use to take a bite out of the trapezoidal wave in the first place.
Finally, there's another function, namely the derivative of the arcsin(sin(x)), which because of it's integral's triangular shape, represents a step function, though is undefined at certain points (unless you interpret the undefined points as zeroes, in which case the Willan's Formulae works just as well assuming you can do the "bite" operation. If you could make the square wave asymmetrical, though, you wouldn't need that, even:
\(\frac{\cos x}{\sqrt{1-\sin^{2}x}}\)
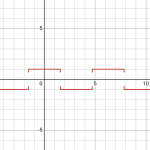
Willans formulae are functions that use brute force to check for primality, by taking some product and all of its products.
Currently, I have been playing with a constructable wave form as follows:
\(p\left(x,x_{1},x_{2}\right)\ =\tanh\left(-k\left(x-\left(2x_{1}\right)\left(x_{2}+2\right)\right)\right)-\tanh\left(-k\left(x-\left(2x_{1}+1\right)\left(x_{2}+2\right)\right)\right)\)
The purple is this:
\(p\left(x,0,0\right)\)
The green is this:
\(\left(1+\sum_{x_{1}=-s}^{s}p\left(x,x_{1},0\right)-p\left(x,0,0\right)\right)\)

As can be seen, This function can be provoked to have zeros at places.
Recently, I also discovered THIS gem, which can be provoked to produce an even more exact structure:
\(k\arcsin\left(\sin\left(x\right)\right)+k\arcsin\left(\sin\left(x+v\right)\right)\)
As can be seen in the following graph, the resulting wave is trapezoidal. at sufficiently high K, with v close enough to but less than pi the system becomes square, however using this to construct a willans/eratosthenes prime counter requires being able to take a bite out of it to make the product.
unfortunately, I've been having a hard time finding a single sum that represents a single "bite" out of such a trapezoidal system:

Is there even some function that continuously defines a line with a single trapezoid out of it? I think it would have to be the sum of two functions that define a single "zag" of a flat line the way the tanh sum does a "steplike shape", but I don't know any way to precisely define just one. It would dramatically speed up the productization time, and would allow an error-free infinite sum.
This connects to Willans methods in the following way:
\(\prod_{n=0}^{s}\left(1+\sum_{x_{1}=-s}^{s}p\left(x,x_{1},n\right)-p\left(x,0,n\right)\right)^{2}\)
\(\sum_{n_{2}=2}^{x}\prod_{n=0}^{s}\left(1+\sum_{x_{1}=-s}^{s}p\left(n_{2},x_{1},n\right)-p\left(n_{2},0,n\right)\right)^{2}\)


Such functions, when taken a bite out of them, represent "is divisible by" as a statement by their zeroes. By squaring such "bitten" wave functions, you can then productize them, representing "is divisible by any prior number".
The trapezoidal function seems the best fit for this, since it doesn't have error past the "shoulder" and while the productization is still expensive, this allows placing the flats so that the shoulders can't interfere with zero-ness of non-prime values between them nor the one-ness at primes. I suspect the trapezoidal function will require high values of K at arbitrarily high values of x, and arbitrarily precise measurements of pi, however, to keep the "shoulders" of higher "mutiple waves" from intruding, and that's assuming there's a function I can use to take a bite out of the trapezoidal wave in the first place.
Finally, there's another function, namely the derivative of the arcsin(sin(x)), which because of it's integral's triangular shape, represents a step function, though is undefined at certain points (unless you interpret the undefined points as zeroes, in which case the Willan's Formulae works just as well assuming you can do the "bite" operation. If you could make the square wave asymmetrical, though, you wouldn't need that, even:
\(\frac{\cos x}{\sqrt{1-\sin^{2}x}}\)