It has been proved that the set of all rational numbers is dense in the set of all real numbers. What this means is that if a and b are real numbers where a < b, then there is a rational number p/q such that a < p/q < b. In other words, there is a rational number between every two real numbers.
If we define the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then is the set {p/q ∈ Q : p ∈ Z and q ∈ N10} dense in the set of real numbers? Observe that the set {p/q ∈ Q : p ∈ Z and q ∈ N10} is a subset of the set of all rational numbers Q. {p/q ∈ Q : p ∈ Z and q ∈ N10} and Q differ in that any element of Q has any nonzero integer in the denominator while {p/q ∈ Q : p ∈ Z and q ∈ N10} is restricted to denominators in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. So for example 1/11 is a rational number but 1/11 is not an element of {p/q ∈ Q : p ∈ Z and q ∈ N10} because the denominator 11 is not in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
My first guess was that no, {p/q ∈ Q : p ∈ Z and q ∈ N10} is not dense in the set of real numbers because the denominator q is restricted to the values in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. I realized that if I could find just one instance of real numbers a and b where a < b and there is no p/q ∈ {p/q ∈ Q : p ∈ Z and q ∈ N10} such that a < p/q < b, then {p/q ∈ Q : p ∈ Z and q ∈ N10} is not dense in the set of real numbers.
My next step involved analyzing the inequality a < p/q < b. I know that q is any natural number from 1 to 10, but what of the integer p? It dawned on me that I can disprove the density of {p/q ∈ Q : p ∈ Z and q ∈ N10} in the set of real numbers by showing exhaustively that any integer p divided by any q ∈ N10 cannot fit between all real numbers a and b.
Returning to the inequality a < p/q < b I multiplied by q getting aq < p < bq. So eureka! I realized that if there is no integer p between aq and bq for real numbers a and b and all q in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then there is no rational number in the set {p/q ∈ Q : p ∈ Z and q ∈ N10} between a and b.
But what real numbers a and b have no such p/q between them? I started out experimenting with crunching numbers in my spreadsheet program, Calc. I figured that a good place to start is with rational numbers like a = 1/11 and b = 3/11 because natural numbers 11 and greater are not in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. So I analyzed 1/11 < p/q < 3/11 and its derivative q/11 < p < 3q/11. Sadly, I found that there are some integers p such that q/11 < p < 3q/11 for some q in N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. What that meant was that there are some elements of {p/q ∈ Q : p ∈ Z and q ∈ N10} between 1/11 and 3/11.
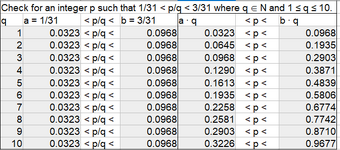
I seemed to be on to something nevertheless. So I tried some more natural numbers greater than 10 and noticed that as their values increased, then the values p/q that fit inside a and b decreased! After more number crunching, I discovered that a = 1/31 and b = 3/31 have no rational numbers p/q between them where q is in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. See the attached spreadsheet. We can then conclude that the set {p/q ∈ Q : p ∈ Z and q ∈ N10} is not dense in the set of real numbers.
It just goes to show what hard work and a love for the truth can do.
If we define the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then is the set {p/q ∈ Q : p ∈ Z and q ∈ N10} dense in the set of real numbers? Observe that the set {p/q ∈ Q : p ∈ Z and q ∈ N10} is a subset of the set of all rational numbers Q. {p/q ∈ Q : p ∈ Z and q ∈ N10} and Q differ in that any element of Q has any nonzero integer in the denominator while {p/q ∈ Q : p ∈ Z and q ∈ N10} is restricted to denominators in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. So for example 1/11 is a rational number but 1/11 is not an element of {p/q ∈ Q : p ∈ Z and q ∈ N10} because the denominator 11 is not in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
My first guess was that no, {p/q ∈ Q : p ∈ Z and q ∈ N10} is not dense in the set of real numbers because the denominator q is restricted to the values in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. I realized that if I could find just one instance of real numbers a and b where a < b and there is no p/q ∈ {p/q ∈ Q : p ∈ Z and q ∈ N10} such that a < p/q < b, then {p/q ∈ Q : p ∈ Z and q ∈ N10} is not dense in the set of real numbers.
My next step involved analyzing the inequality a < p/q < b. I know that q is any natural number from 1 to 10, but what of the integer p? It dawned on me that I can disprove the density of {p/q ∈ Q : p ∈ Z and q ∈ N10} in the set of real numbers by showing exhaustively that any integer p divided by any q ∈ N10 cannot fit between all real numbers a and b.
Returning to the inequality a < p/q < b I multiplied by q getting aq < p < bq. So eureka! I realized that if there is no integer p between aq and bq for real numbers a and b and all q in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then there is no rational number in the set {p/q ∈ Q : p ∈ Z and q ∈ N10} between a and b.
But what real numbers a and b have no such p/q between them? I started out experimenting with crunching numbers in my spreadsheet program, Calc. I figured that a good place to start is with rational numbers like a = 1/11 and b = 3/11 because natural numbers 11 and greater are not in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. So I analyzed 1/11 < p/q < 3/11 and its derivative q/11 < p < 3q/11. Sadly, I found that there are some integers p such that q/11 < p < 3q/11 for some q in N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. What that meant was that there are some elements of {p/q ∈ Q : p ∈ Z and q ∈ N10} between 1/11 and 3/11.
I seemed to be on to something nevertheless. So I tried some more natural numbers greater than 10 and noticed that as their values increased, then the values p/q that fit inside a and b decreased! After more number crunching, I discovered that a = 1/31 and b = 3/31 have no rational numbers p/q between them where q is in the set N10 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. See the attached spreadsheet. We can then conclude that the set {p/q ∈ Q : p ∈ Z and q ∈ N10} is not dense in the set of real numbers.
It just goes to show what hard work and a love for the truth can do.