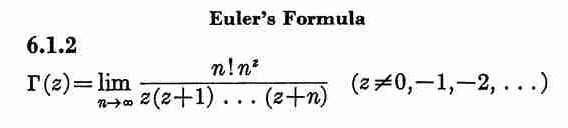Extending Factorials

[lpetrich]

I have fond memories from long ago of Abramowitz and Stegun's fat book "Handbook of Mathematical Functions". It is online at Abramowitz and Stegun: Handbook of Mathematical Functions

One of the chapters is "Gamma Function and Related Functions", about an extension of the factorial function. To understand that extension, consider an integral representation of it:

\( n! = \int_0^\infty t^n e^{-t} dt \)

It is easy to find 0! from it, and also to find the factorial recurrence relation, n! = n*(n-1)! from it. One does integration by parts:

\( n! = \int t^n d(-e^{-t}) = - t^n e^{-t} + n \int t^{n-1} e^{-t} dt \)

Can we extend this integral representation to non-integer n? We can indeed do so, and that is the Euler gamma function:

\( n! = \Gamma(n+1) \)

\( \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt \)

One can express the exponential function as the limit of a polynomial function:

\( \Gamma(z) = \lim_{n\to\infty} \int_0^n t^{z-1} \left( 1 - \frac{t}{n} \right)^n dt = \lim_{n\to\infty} \frac{n! n^z}{\prod_{k=0}^n (z+k)} \)

This is Euler's formula, and it yields Euler's infinite product:

\( \frac{1}{\Gamma(z)} = z e^{\gamma z} \prod_{n=1}^\infty \left( 1 + \frac{z}{n} \right) e^{-z/n} \)

where γ is the Euler-Mascheroni constant:

\( \gamma = 0.57721\ 56649 \ldots \)

 

[lpetrich]

The derivative of the logarithm of the Euler gamma function is the psi or digamma function:

\( \psi(z) = \frac{d}{dz} (\log \Gamma(z) ) \)

From Euler's formula,

\( \psi(z) = \lim_{n\to\infty} \left( \log n - \sum_{k=0}^n \frac{1}{z+k} \right) = - \gamma - \frac{1}{z} + \sum_{n=1}^\infty \frac{z}{n(n+z)} \)

Taking another derivative gives the trigamma function,

\( \psi'(z) = \sum_{n=0}^\infty \frac{1}{(z+n)^2} \)

Or more generally, the polygamma function,

\( \psi^{(n)}(z) = (-1)^{n+1} n! \sum_{k=0}^\infty \frac{1}{(z+k)^{n+1}} \)

This gives us an integral form:

\( \psi^{(n)}(z) = (-1)^{n+1} \int_0^{\infty} \frac{t^n e^{-z t}}{1 - e^{-t}} dt \)

Integrating it gives us

\( \psi(z) = \int_0^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-z t}}{1 - e^{-t}} \right) dt \)

and

\( \log \Gamma(z) = \int_0^\infty \left( (z-1) e^{-t} - \frac{e^{-t} - e^{-z t}}{1 - e^{-t}} \right) \frac{dt}{t} \)

The last one is easy to verify for z = 1 and z = 2. One can also verify the recurrence relation

\( \log \Gamma(z+1) = \log \Gamma(z) + \log z \)

 

[lpetrich]

One can find a reflection formula:

\( \Gamma(z) \Gamma(1-z) = \frac{\pi}{\sin (\pi z)} \)

Also Gauss's multiplication formula:

\( \Gamma(n z) = (2\pi)^{(1-n)/2} n^{n z - 1/2} \prod_{k=0}^{n-1} \Gamma \left( z + \frac{k}{n} \right) \)

One can get an interesting result with n = 2 and z = 1/2 in the multiplication formula, and z = 1/2 in the reflection formula:

\( \Gamma(1/2) = \sqrt{\pi} \)

 

[lpetrich]

The recurrence:
\( \psi(z+1) = \psi(z) + \frac{1}{z} \)
and
\( \psi^{(n)}(z+1) = \psi^{(n)}(z) + \frac{(-1)^n n!}{z^{n+1}} \)

The reflection formula uses this infinite product for the sine:
\( \sin (\pi z) = \pi z \prod_{n=1}^{\infty} \left( 1 - \frac{z^2}{n^2} \right) \)

There is a similar formula for the cosine:
\( \cos (\pi z) = \prod_{n=1}^{\infty} \left( 1 - \frac{z^2}{(n-1/2)^2} \right) \)

 

[Kharakov]

The Gamma function is one of the functions connecting discrete and continuous mathematics.

Euler's Formula (from A & S) is a nice, fully written out version. Loren had it, but I didn't see it at first when I glanced over his formulas. I think this version looks nicer:






1) Weird. I couldn't post in this thread earlier. Maybe I timed out when reading some other site. Reopened the thread, and it seems to work...

2) Now it says "the message you have entered is too short". ETA: fixed. While the editor allows you to copy and paste an image, whenever you do that (instead of using the image button), it gives you the "message is less than 2 characters" popup.


3) I think all of it was me copying and pasting an image. Both errors. One time I had written out a decent sized post.. and lost the whole thing when I clicked "go advanced". It showed a blank edit window. Copied stuff into it, and it sort of worked, tried to back out and go forward in the browser, and lost everything. mehh. That used to fix it here. Maybe new version of firefox, or ES7? I dunno.

 

[lpetrich]

Here is Euler's formula, for deriving the reflection formula:
\( \Gamma(z) = \lim_{n\to\infty} \frac{n^z}{z (1+z)(1+z/2) \cdots (1+z/n)} \)

\( \Gamma(1+z) = \lim_{n\to\infty} \frac{n^z}{(1+z)(1+z/2) \cdots (1+z/n)} \)


\( \Gamma(1-z) = \lim_{n\to\infty} \frac{n^{-z}}{(1-z)(1-z/2) \cdots (1-z/n)} \)

\( \Gamma(z) \Gamma(1-z) = \frac{1}{z (1 - z^2) (1 - z^2/2^2) (1 - z^2/3^2) \cdots} = \frac{\pi}{\sin (\pi z)} \)

 

[lpetrich]

Now the multiplication formula.
\( \sum_{k=0}^{n-1} \psi^{(m)}(z+k/n) = \sum_{k=0}^{n-1} (-1)^{m+1} \int_0^\infty \frac{t^m e^{-(z+k/n)t}}{1 - e^{-t}} dt \)

\( \sum_{k=0}^{n-1} e^{-(z+k/n)t} = e^{-z t} \frac{1 - e^{-t}}{1 - e^{-t/n}} \)

\( (-1)^{m+1} \int_0^\infty \frac{t^m e^{-z t}}{1 - e^{-t/n}} dt = n^{m+1} \psi^{(m)}(n z) \)

In summary,

\( \psi^{(m)}(n z) = n^{-(m+1)} \sum_{k=0}^{n-1} \psi^{(m)}(z+k/n) \)

That gives us

\( \psi(n z) = C_0(n) + \frac{1}{n} \sum_{k=0}^{n-1} \psi(z+k/n) \)

and

\( \log \Gamma(n z) = n z C_0(n) + C_1(n) + \sum_{k=0}^{n-1} \log\Gamma(z+k/n) \)

Here, C₀ and C₁ are constants of integration, and we must find those constants.

 

[lpetrich]

\( \sum_{k=0}^{n-1} \psi(z + k/n) = \sum_{k=0}^{n-1} \int_{\epsilon}^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-t} - e^{- (z+k/n) t}}{1 - e^{-t}} \right) dt = n \int_{\epsilon}^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-t}}{1 - e^{-t}} \right) dt + \int_{\epsilon}^\infty \frac{e^{-z}}{1 - e^{-t/n}} dt \)

where ε has limit 0.

Multiply t by n in the second integral on the right:
\( n \int_{n \epsilon}^\infty \frac{e^{- n z t}}{1 - e^{-t}} dt = n \int_{\epsilon}^\infty \frac{e^{- n z t}}{1 - e^{-t}} dt - n \int_{\epsilon}^{n \epsilon} \frac{dt}{t} \)

The second integral evaluates to n*log, and we find

\( \psi(n z) = \log n + \frac{1}{n} \sum_{k=0}^{n-1} \psi(z + k/n) \)

This gives us C₀.

 

[lpetrich]

\( \sum_{k=0}^{n-1} \log \Gamma(z+k/n) = \int_{\epsilon}^\infty \left( (n z - (n+1)/2) e^{-t} - n \frac{e^{-t}}{1 - e^{-t}} + \frac{e^{- z t}}{1 - e^{-t/n}} \right) \frac{dt}{t} \)

with the integral including the multiplied gamma function:
\( \log \Gamma(n z) + \int_{\epsilon}^\infty \left( - ((n-1)/2) e^{-t} - (n-1) \frac{e^{-t}}{1 - e^{-t}} + \frac{e^{- z t}}{1 - e^{-t/n}} - \frac{e^{-n z t}}{1 - e^{-t}} \right) \frac{dt}{t} \)

One can expand the integral as a series in z, and powers of z greater than 1 will vanish, because the integrand has no divergences in it in that case. It is the presence of those divergences that makes nonzero coefficients of 1 and z. The part with z is

\( \int_{\epsilon}^\infty \left( \frac{- z t}{1 - e^{-t/n}} - \frac{-n z t}{1 - e^{-t}} \right) \frac{dt}{t} = z \int_{\epsilon}^\infty \left( - \frac{1}{1 - e^{-t/n}} + \frac{n}{1 - e^{-t}} \right) dt = - n z \int_{\epsilon}^{n \epsilon} \frac{dt}{t} = - n z \log n \)

\( \log \Gamma(n z) - n z \log n+ \int_{\epsilon}^\infty \left( - ((n-1)/2) e^{-t} - (n-1) \frac{e^{-t}}{1 - e^{-t}} + \frac{1}{1 - e^{-t/n}} - \frac{1}{1 - e^{-t}} \right) \frac{dt}{t} \)

Simplifying the integral gives us

\( \log \Gamma(n z) - n z \log n+ \int_{\epsilon}^\infty \left( (n-1) - ((n-1)/2) e^{-t} + \frac{1}{1 - e^{-t/n}} - \frac{n}{1 - e^{-t}} \right) \frac{dt}{t} \)

It's necessary to reshuffle the integral so we can do some cancellation on it:
\( \int_{\epsilon}^\infty \left[ \frac12 (e^{-t} - e^{-t/n}) + \left( \frac{1}{1 - e^{-t/n}} - \frac{n}{t} - 1 + \frac12 e^{-t/n} \right) - \left( \frac{n}{1 - e^{-t}} - \frac{n}{t} - n + \frac{n}{2} e^{-t} \right) \right] \frac{dt}{t} \)

The first term in parens can be turned into the integral
\( - \frac12 \int_{\epsilon/n}^{\epsilon}\frac{e^{-t}}{t} dt = - \frac12 \log n \)

The second and third terms in parens are well-behaved for small t, and the second one can be shifted by taking t -> n*t. This gives us
\( - \frac12 \log n - (n - 1) \int_0^\infty \left( \frac{1}{1 - e^{-t}} - \frac{1}{t} - 1 + \frac12 e^{-t} \right) \frac{dt}{t} \)

The remaining integral is equal to -(1/2)*log(2*pi)

I don't know why the sign on (1/2)*log is - instead of + as it's supposed to be -- any typo anywhere?

 

[lpetrich]

These formulas look vertically compressed because they were all done with LaTeX's default line layout: \textstyle. So I've decided to redo them with \displaystyle.

 

[lpetrich]

Integral for the factorial function: \( \displaystyle{ n! = \int_0^\infty t^n e^{-t} dt } \)

It is easy to show that 0! = 1, and also to find the factorial recurrence relation, \(n! = n (n-1)!\) from it. One does integration by parts:

\( \displaystyle{ n! = \int_{t=0}^{t=\infty} t^n d(-e^{-t}) = \left( - t^n e^{-t} \right)_{t=0}^{t=\infty} + n \int_0^\infty t^{n-1} e^{-t} dt } \)

Can we extend this integral representation to non-integer n? We can indeed do so, and that is the Euler gamma function:

\( n! = \Gamma(n+1) \) where \( \displaystyle{ \Gamma(z) = \int_0^\infty t^{z-1} e^{-t} dt } \)

One can express the exponential function as the limit of a polynomial function:

\( \displaystyle{ \Gamma(z) = \lim_{n\to\infty} \int_0^n t^{z-1} \left( 1 - \frac{t}{n} \right)^n dt = \lim_{n\to\infty} \frac{n! n^z}{\prod_{k=0}^n (z+k)} } \)

This is Euler's formula, and it yields Euler's infinite product:

\( \displaystyle{ \frac{1}{\Gamma(z)} = z e^{\gamma z} \prod_{n=1}^\infty \left( 1 + \frac{z}{n} \right) e^{-z/n} } \)

where γ is the Euler-Mascheroni constant:

\( \displaystyle{ \gamma = \lim_{n\to\infty} \left( \sum_{k=1}^n \frac{1}{k} - \log n \right) = 0.57721\ 56649 \ldots } \)

 

[lpetrich]

The derivative of the logarithm of the Euler gamma function is the psi or digamma function:

\( \displaystyle{ \psi(z) = \frac{d}{dz} (\log \Gamma(z) ) } \)

From Euler's formula,

\( \displaystyle{ \psi(z) = \lim_{n\to\infty} \left( \log n - \sum_{k=0}^n \frac{1}{z+k} \right) = - \gamma - \frac{1}{z} + \sum_{n=1}^\infty \frac{z}{n(n+z)} } \)

Taking another derivative gives the trigamma function,

\( \displaystyle{ \psi'(z) = \sum_{n=0}^\infty \frac{1}{(z+n)^2} } \)

Or more generally, the polygamma function,

\( \displaystyle{ \psi^{(m)}(z) = (-1)^{m+1} m! \sum_{n=0}^\infty \frac{1}{(z+n)^{m+1}} } \)

This gives us an integral form:

\( \displaystyle{ \psi^{(m)}(z) = (-1)^{m+1} \int_0^{\infty} \frac{t^m e^{-z t}}{1 - e^{-t}} dt } \)

Integrating it gives us

\( \displaystyle{ \psi(z) = \int_0^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-z t}}{1 - e^{-t}} \right) dt } \)

and

\( \displaystyle{ \log \Gamma(z) = \int_0^\infty \left( (z-1) e^{-t} - \frac{e^{-t} - e^{-z t}}{1 - e^{-t}} \right) \frac{dt}{t} }\)

The last one is easy to verify for z = 1 and z = 2. One can also verify the recurrence relation

\( \log \Gamma(z+1) = \log \Gamma(z) + \log z \)

 

[lpetrich]

One can find a reflection formula:

\( \displaystyle{ \Gamma(z) \Gamma(1-z) = \frac{\pi}{\sin (\pi z)} } \)

Also Gauss's multiplication formula:

\( \displaystyle{ \Gamma(n z) = (2\pi)^{(1-n)/2} n^{n z - 1/2} \prod_{k=0}^{n-1} \Gamma \left( z + \frac{k}{n} \right) } \)

One can get an interesting result with n = 2 and z = 1/2 in the multiplication formula, and z = 1/2 in the reflection formula:

\( \Gamma(1/2) = \sqrt{\pi} \)

 

[lpetrich]

The add-1 recurrence extended to the digamma and polygamma functions:
\( \displaystyle{ \psi(z+1) = \psi(z) + \frac{1}{z} } \)
and
\( \displaystyle{ \psi^{(m)}(z+1) = \psi^{(m)}(z) + \frac{(-1)^m m!}{z^{m+1}} } \)

The reflection formula can be derived with this infinite product for the sine:
\( \displaystyle{ \sin (\pi z) = \pi z \prod_{n=1}^{\infty} \left( 1 - \frac{z^2}{n^2} \right) } \)

There is a similar formula for the cosine:
\( \displaystyle{ \cos (\pi z) = \prod_{n=1}^{\infty} \left( 1 - \frac{z^2}{(n-1/2)^2} \right) } \)

 

[lpetrich]

Here is Euler's formula, in a form convenient for deriving the reflection formula:
\( \displaystyle{ \Gamma(z) = \lim_{n\to\infty} \frac{n^z}{z \prod_{k=1}^n (1 + z/k)} } \)

\( \displaystyle{ \Gamma(z) \Gamma(1-z) = - z \Gamma(z) \Gamma(-z) = \frac{1}{z \prod_{k=1}^n (1 - (z/k)^2) \cdots} = \frac{\pi}{\sin (\pi z)} } \)

Taking the derivative,

\( \displaystyle{ \psi(z) - \psi(1-z) = \pi \cot \pi z } \)

Further derivatives don't have any simple formula.

 

[lpetrich]

Turning to the multiplication formula, we first take multiple derivatives of the gamma function, because it's easier to work with the polygamma function.
\( \displaystyle{ \sum_{k=0}^{n-1} \psi^{(m)}(z+k/n) = \sum_{k=0}^{n-1} (-1)^{m+1} \int_0^\infty \frac{t^m e^{-(z+k/n)t}}{1 - e^{-t}} dt } \)

Exchanging the sum and the integral,
\( \displaystyle{ \sum_{k=0}^{n-1} e^{-(z+k/n)t} = e^{-z t} \frac{1 - e^{-t}}{1 - e^{-t/n}} } \)

Inserting it in,
\( \displaystyle{ (-1)^{m+1} \int_0^\infty \frac{t^m e^{-z t}}{1 - e^{-t/n}} dt = n^{m+1} \psi^{(m)}(n z) } \)

In summary,
\( \displaystyle{ \psi^{(m)}(n z) = n^{-(m+1)} \sum_{k=0}^{n-1} \psi^{(m)}(z+k/n) } \)

Integrating \( \psi^{(1)}(z) \) over z gives us
\( \displaystyle{ \psi(n z) = C_0(n) + \frac{1}{n} \sum_{k=0}^{n-1} \psi(z+k/n) } \)

and integrating further gives us
\( \displaystyle{ \log \Gamma(n z) = n z C_0(n) + C_1(n) + \sum_{k=0}^{n-1} \log\Gamma(z+k/n) } \)

The C's are constants of integration, but constants of integration relative to z, and that makes them functions of n.

 

[lpetrich]

Let us first find \(C_0(n)\)
\( \displaystyle{ C_0(n) = \psi(nz) - \frac{1}{n} \sum_{k=0}^{n-1} \psi(z + k/n) } \)

Using their integral forms gives us, with nonzero lower bound because of the cancellation of infinities at t = 0,
\( \displaystyle{ \int_{\epsilon}^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-t} - e^{- nzt}}{1 - e^{-t}} \right) dt - \frac{1}{n} \sum_{k=0}^{n-1} \int_{\epsilon}^\infty \left( \frac{e^{-t}}{t} - \frac{e^{-t} - e^{- (z+k/n) t}}{1 - e^{-t}} \right) dt } \)

where the lower bound ε has limit 0.

The parts independent of z cancel out, giving us
\( \displaystyle{ \int_{\epsilon}^\infty \left( \frac{e^{- nzt}}{1 - e^{-t}} \right) dt - \frac{1}{n} \sum_{k=0}^{n-1} \int_{\epsilon}^\infty \left( \frac{e^{- (z+k/n) t}}{1 - e^{-t}} \right) dt } \)

Doing the sum in the second integral gives us
\( \displaystyle{ \int_{\epsilon}^\infty \left( \frac{e^{- nzt}}{1 - e^{-t}} \right) dt - \frac{1}{n} \sum_{k=0}^{n-1} \int_{\epsilon}^\infty \left( \frac{e^{- zt}}{1 - e^{-t/n}} \right) dt } \)

Multiplying t by n in the second integral gives us
\( \displaystyle{ \int_{\epsilon}^\infty \left( \frac{e^{- nzt}}{1 - e^{-t}} \right) dt - \int_{n\epsilon}^\infty \left( \frac{e^{- nzt}}{1 - e^{-t}} \right) dt = \int_{\epsilon}^{n\epsilon} \left( \frac{e^{- nzt}}{1 - e^{-t}} \right) dt = \int_{\epsilon}^{n\epsilon} \frac{dt}{t} = \log n\epsilon - \log \epsilon = \log n} \)

Thus, \(C_0(n) = \log n\) and
\( \displaystyle{ \psi(nz) = \log n + \frac{1}{n} \sum_{k=0}^{n-1} \psi(z + k/n) } \)

 

[lpetrich]

Finding \(C_1(n)\) is more difficult, but one proceeds in the same way.

The target value
\( \displaystyle{ \log \Gamma(nz) = \int_{\epsilon}^\infty \left( (nz - 1) e^{-t} - \frac{e^{-t} - e^{- nzt}}{1 - e^{-t}} \right) \frac{dt}{t} }\)

The product value with the \(C_0(n)\) integral
\( \displaystyle{ nz \log n + \sum_{k=0}^{n-1} \log \Gamma(z+k/n) = \int_{\epsilon}^\infty \left( (n z - (n+1)/2) e^{-t} - n \frac{e^{-t}}{1 - e^{-t}} + \frac{e^{- z t}}{1 - e^{-t/n}} \right) \frac{dt}{t} } \)

Their difference:
\( \displaystyle{ -nz \log n - \int_{\epsilon}^\infty \left( - ((n-1)/2) e^{-t} - (n-1) \frac{e^{-t}}{1 - e^{-t}} + \frac{e^{- z t}}{1 - e^{-t/n}} - \frac{e^{-n z t}}{1 - e^{-t}} \right) \frac{dt}{t} } \)

Reshuffling the integrand:
\( \displaystyle{ - (n-1) \left( \frac{e^{-t}}{1 - e^{-t}} - \frac{1}{t} \right) + \left( \frac{e^{- z t}}{1 - e^{-t/n}} - \frac{n}{t} + \right) - \left( \frac{e^{-n z t}}{1 - e^{-t}} - \frac{1}{t} \right) } \)

The second and last terms give us
\( \displaystyle{ - \int_{\epsilon}^\infty \left( \frac{e^{- z t}}{1 - e^{-t/n}} - \frac{n}{t} \right) \frac{dt}{t} + \int_{\epsilon}^\infty \left( \frac{e^{-n z t}}{1 - e^{-t}} - \frac{1}{t} \right) \frac{dt}{t} } \)

Multiplying t by n in the first integral gives us
\( \displaystyle{ \int_{\epsilon}^{n\epsilon} \left( \frac{e^{-n z t}}{1 - e^{-t}} - \frac{1}{t} \right) \frac{dt}{t} = \left( \frac{1}{2} - nz \right) \log n } \)

That difference becomes
\( \displaystyle{ (n-1) \int_0^\infty \left( \frac{e^{-t}}{1 - e^{-t}} - \frac{1}{t} + \frac{1}{2} e^{-t} \right) \frac{dt}{t} = -(n-1) \log C } \)

So
\( \displaystyle{ \Gamma(nz) = C^{n-1} n^{nz-1/2} \prod_{k=0}^{n-1} \Gamma(z + k/n) } \)

 

[lpetrich]

For finding C, we use some special values: n = 2, z = 1/2. That gives us

\( \Gamma(2) = 1 = 2^{1/2} C \cdot \Gamma(1/2) \Gamma(1) = 2^{1/2} \pi^{1/2} C \)

giving us \( C = 1 / \sqrt{2\pi} \)
and
\( \displaystyle{ \log C = - \frac{1}{2} \log (2\pi) = \int_0^\infty \left( \frac{e^{-t}}{1 - e^{-t}} - \frac{1}{t} + \frac{1}{2} e^{-t} \right) \frac{dt}{t} } \)
and
\( \displaystyle{ \Gamma(nz) = \frac{n^{nz-1/2}}{(2\pi)^{(n-1)/2}} \prod_{k=0}^{n-1} \Gamma(z + k/n) } \)

 

[lpetrich]

Related to the gamma function is the beta function:

\( \displaystyle{ B(s,t) = \int_0^1 x^{s-1} (1-x)^{t-1} \, dt = \frac{\Gamma(s) \Gamma(t)}{\Gamma(s+t)} } \)

If one integrates over only part of these functions' domains of integration, one finds the incomplete gamma and beta functions.

The cumulative forms of some probability distributions are incomplete gamma and beta functions: 1.3.6.6. Gallery of Distributions and  List of probability distributions