Math Quiz Thread

[steve_bnk]

A thread for math problems, not puzzles.

Here s a little problem I just worked through today for something.


Given a sine wave at a frequency of20,000 Hertz and an amplitude of 20 what is the maximum rate ofchange?


20*sin(2P*If*t)

 

[Kharakov]

At certain inflection points, isn't the maximum instantaneous rate of change positive or negative infinity for both cosine and sin?

I might be confusing terms though- do you mean something like the rate of change of curvature, like in the trough or at the peak?

 

[steve_bnk]

At certain inflection points, isn't the maximum instantaneous rate of change positive or negative infinity for both cosine and sin?

I might be confusing terms though- do you mean something like the rate of change of curvature, like in the trough or at the peak?

Just as stated without giving the problem away.

Calc 101 and trig functions.

 

[Juma]

A thread for math problems, not puzzles.

Here s a little problem I just worked through today for something.


Given a sine wave at a frequency of20,000 Hertz and an amplitude of 20 what is the maximum rate ofchange?


20*sin(2P*If*t)

If f(x) = g(h(x)) then f'(x)=g'(h(x))*h'(x)
your signal is y = 20sin(40,000pi*t) so the rate of change is 800,000*pi*cos(40.000pi*t) and since max of cos is 1 the max rate of change is 800,000*pi.

 

[beero1000]

Compute (by hand) the value of \(\frac{1000000}{\sin(\frac{\pi}{5000}) +\sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000})}\) to the nearest thousandth.


If \(P = \lim_{n \to\infty} \prod_{k=1}^n (1 + \frac{1}{2^k})\), prove (by hand) that \(P\) converges to a number such that \(2.3< P < 2.5\).

 

[steve_bnk]

A thread for math problems, not puzzles.

Here s a little problem I just worked through today for something.


Given a sine wave at a frequency of20,000 Hertz and an amplitude of 20 what is the maximum rate ofchange?


20*sin(2P*If*t)

If f(x) = g(h(x)) then f'(x)=g'(h(x))*h'(x)
your signal is y = 20sin(40,000pi*t) so the rate of change is 800,000*pi*cos(40.000pi*t) and since max of cos is 1 the max rate of change is 800,000*pi.

s
Sort of.


f'(u) = f(u)*du the chain rule.


F = 20,000hz
Amplitude 20 volts
t in seconds


derivative of the sin is cos.
u = 2PI*f*t
du = 2PI*f (d(kx) = k)


f(t) = 20 * sin(2PI*f*t)
f'(t) = 20*2PI*f*cos(2PI*f*t)


max rate of change of the sine will be when the derivative cos is 1 at t = 0.


f' max = 20*2PI*f*cos(2PI*f*0)


f' max = 20*2PI*f*1 = 2513274.1volts/second or rounded 2.5 mega volts per second.


I am working on an audio amp and neededto know the maximum slew rate needed for the amplifier to pass a20khz signal.


People really do use calculus.


The minimum will be when cos = 0 atPi/4 or 50 micro seconds/4.

 

[steve_bnk]

Compute (by hand) the value of \(\frac{1000000}{\sin(\frac{\pi}{5000}) +\sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000})}\) to the nearest thousandth.


If \(P = \lim_{n \to\infty} \prod_{k=1}^n (1 + \frac{1}{2^k})\), prove (by hand) that \(P\) converges to a number such that \(2.3< P < 2.5\).

I give up, you got me stumped with a problem from theoretical math that would take me weeks to months to work through..

That is not a math quiz, that is more like a term paper..

 

[beero1000]

Compute (by hand) the value of \(\frac{1000000}{\sin(\frac{\pi}{5000}) +\sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000})}\) to the nearest thousandth.


If \(P = \lim_{n \to\infty} \prod_{k=1}^n (1 + \frac{1}{2^k})\), prove (by hand) that \(P\) converges to a number such that \(2.3< P < 2.5\).

I give up, you got me stumped with a problem from theoretical math that would take me weeks to months to work through..

That is not a math quiz, that is more like a term paper..

Each has a near trivial solution, easily done by hand. Nothing more than basic calculus and series.

 

[steve_bnk]

Compute (by hand) the value of \(\frac{1000000}{\sin(\frac{\pi}{5000}) +\sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000})}\) to the nearest thousandth.


If \(P = \lim_{n \to\infty} \prod_{k=1}^n (1 + \frac{1}{2^k})\), prove (by hand) that \(P\) converges to a number such that \(2.3< P < 2.5\).

I give up, you got me stumped with a problem from theoretical math that would take me weeks to months to work through..

That is not a math quiz, that is more like a term paper..

Each has a near trivial solution, easily done by hand. Nothing more than basic calculus and series.

Beyond me. It would take me weeks to figure out how to approach the problem. I vaguely remember tests for convergence and taking derivatives of terms, but it is long gone.

Derivatives of sines and cosines are both trivial and foundational appearing everywhere in mechanical and electrical dynamic systems. Same with all of basic clculus such as the chain rule.

 

[Kharakov]

Compute (by hand) the value of \(\frac{1000000}{\sin(\frac{\pi}{5000}) +\sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000})}\) to the nearest thousandth.

Umm... can you divide by zero now? I really want to, but.... Whoops... cosine.. and that would have been -1000000...

If \(P = \lim_{n \to\infty} \prod_{k=1}^n (1 + \frac{1}{2^k})\), prove (by hand) that \(P\) converges to a number such that \(2.3< P < 2.5\).

Do I have to do the math, or can I just assume the silver ratio of \(\sqrt{2}+1\)?

 

[Kharakov]

Beero- you sure you didn't mean 10000/5000 pi for the last term of the series for the easy cancellation?

 

[beero1000]

Beero- you sure you didn't mean 10000/5000 pi for the last term of the series for the easy cancellation?

No. If the sum went to 10000pi/5000, then it really would be division by zero.

 

[Kharakov]

Ok, it would be easy if all the sins were squared- we end up with 1000000/2500. The thing is, they aren't. If it was cosine, we'd end up with -1 on the bottom. So I'm stumped at whatever trivial identity you're talking about.

 

[beero1000]

Ok, it would be easy if all the sins were squared- we end up with 1000000/2500. The thing is, they aren't. If it was cosine, we'd end up with -1 on the bottom. So I'm stumped at whatever trivial identity you're talking about.

Hint for the first one.

Show

 

[AdamWho]

This is a tricky calculus problem that my students had some problems with.

So does the sum converge or diverge?

\(\sum_{n=1}^{\infty }\frac{nln(n)}{(n+1)^{3}}\)

 

[Kharakov]

Hint for the first one.

Show

View attachment 260

Yeah.. problem is that the sum of sins is

Show

~ 3183.1

so I don't get what you're getting at... although I looked it up and see that I could say

Show

1000000/2500*pi

which is within your constraints.

 

[steve_bnk]

kharakov beat me to it but.

Show

I imagine you are looking forsomething like 1e6/[5000*k] where k = sin(n*pi/50000).


if you plot sin(n*2*pi/50000) for n = 1to 5000 you get a sine wave with 5000 points and a sum of zero.




This is a routine I use to create amathematical sine wave.


//-------------------------------------------------------------------------------------
// Creates a sine wave
function [s_wave] = make_sin(n_points,_amplitude, _cycles)
for nn = 1:n_points*_cycles;
s_wave(nn) = _amplitude*sin(nn*6.28/n_points);
end;
endfunction;
//-------------------------------------------------------------------------------------\\


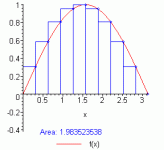
What you have in the denominator is ahalf sine with amplitude = 1 and points = 5000. The sum isapproximately 3183, which I believe amounts to a line integral. I didit numerically. A bit of work but can be done by hand.


http://en.wikipedia.org/wiki/Line_integral




//-------------------------------------------------------------------------------------
// berro's half sin
function [s_wave] = make_sin(n_points,_amplitude)
for nn = 1:n_points;
s_wave(nn) = _amplitude*sin(nn*PI/n_points);
end;
endfunction;
//-------------------------------------------------------------------------------------\\


Plot the denominator in whatever toolyou use.


What I think you want is something like this. Sine repeats periodic in multiples of 2PI staring at PI/2.


1000000/[sin(1*pi/2) + sin (5*pi/2) +sin (9*pi/2) …sin (20001*pi/2) ]


1 +1 + 1 ….

 

[beero1000]

Hint for the first one.

Show

View attachment 260

Yeah.. problem is that the sum of sins is

Show

~ 3183.1

so I don't get what you're getting at... although I looked it up and see that I could say

Show

1000000/2500*pi

which is within your constraints.

Answer:

Show

The sum \(\sin(\frac{\pi}{5000}) + \sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000})\) is actual a Riemann sum \(\sum_{i=1}^{5000} \frac{5000}{\pi}\sin(\frac{i\pi}{5000}) \Delta x\) with \(\Delta x = \frac{\pi}{5000}\). It is essentially the integral \(\int_{0}^\pi \frac{5000}{\pi}\sin(x) dx\) (remember cutting areas under curves into rectangles in calculus? The limit of the area of the rectangles is the integral). So \(\sin(\frac{\pi}{5000}) + \sin(\frac{2\pi}{5000}) + \dots + \sin(\frac{5000\pi}{5000}) \approx \int_0^{\pi} \frac{5000}{\pi} \sin(x) dx = \frac{10000}{\pi}\). The difference between the Riemann sum and the integral is tiny and can be quantified to be less than around 0.001 out of 3000+ (the overestimation between 0 and pi/2 is almost entirely cancelled out by the underestimation between pi/2 and pi), so

\(\frac{1000000}{\sin(\frac{\pi}{5000})+\dots+\sin(\frac{5000\pi}{5000})} \approx \frac{1000000}{\int_0^\pi \frac{5000}{\pi} \sin(x) dx} = \frac{1000000}{\frac{10000}{\pi}} = 100\pi\).

Therefore, the value is 314.159.

 

[beero1000]

This is a tricky calculus problem that my students had some problems with.

So does the sum converge or diverge?

\(\sum_{n=1}^{\infty }\frac{nln(n)}{(n+1)^{3}}\)

Answer:

Show

Converges. All but finitely many terms are bounded above by the convergent p-series \(\sum_{n=1}^\infty \frac{1}{n^{1.5}}\)

 

[steve_bnk]

Calculate by hand without a calculator.


6.6344/[sin(1*pi/2) + sin(5*pi/2) +sin(9*pi/2)....sin(41*pi/2)]

Show

sin(1*pi/2) = 1, periodic inmultiples of 4*pi/2. 10 terms sums to 10.


Answer 6.6344/10 = .66344