Math Quiz Thread

[beero1000]

I'll use row rank here.

The first two rows of that matrix can be used to calculate the third one: - (first) + 2*(second). One can make a rank-1 matrix from each of those first two rows, thus giving two rank-1 matrices.
{{1, 1, 0}}
{{1, 3, 4}}
with
{{1, 5, 8}} = 2*{{1, 3, 4}} - {{1, 1, 0}}

More generally, any row of any matrix can form a rank-1 matrix. It's {row}.

Yup. The SVD gives the best possible such decomposition i.e. if the sum of rank 1 matrices is truncated, the resulting approximation is closest (among all such sums) to the original matrix.

If a 3 x 3 matrix A has eigenvalues 0, 1, and 2, what are the eigenvalues of (A²+I)^-1?

In general, if a matrix A has an eigenvalue λ, then F(A) has a corresponding eigenvalue, f(λ).
Thus, 0, 1, 2 correspond to 1, 1/2, 1/5.

How many different Jordan forms represent the class of 2 x 2 binary matrices?

Eight:
\( \left( \begin{array}{cc} -1 & 0 \\ 0 & 1 \\ \end{array} \right), \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right), \left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ \end{array} \right), \left( \begin{array}{cc} 0 & 0 \\ 0 & 2 \\ \end{array} \right), \left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \\ \end{array} \right), \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right), \left( \begin{array}{cc} 1 & 1 \\ 0 & 1 \\ \end{array} \right), \left( \begin{array}{cc} \frac{1}{2} \left(1-\sqrt{5}\right) & 0 \\ 0 & \frac{1}{2} \left(1+\sqrt{5}\right) \\ \end{array} \right) \)

Found with Mathematica:

TeXForm /@ Union[JordanDecomposition[Partition[#, 2]][[2]] & /@ Tuples[{0, 1}, 4]]

A nice way to see that without explicitly computing the representatives is: The trace is 0, 1, or 2 and for each trace value, the determinant has two possible values, so there are 6 possible characteristic polynomials. Two of these also represent classes of non-diagonalizable matrices (corresponding to eigenvalue pairs (0,0) and (1,1)). Therefore, there are 8 different families.

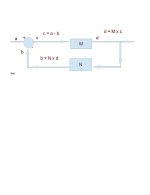
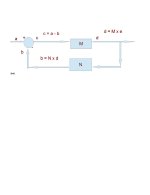
Transposition of n x n matrices is a linear mapping. If every (finite-dimensional) linear mapping has a matrix representation, why can't we say that there is a matrix A such that AM = M^T for every M? What is the correct statement?

You have to flatten M. Transposing is then interchanging the components of this M vector in a suitable way.

A.M = M^T gives A = M^T.M^-1, and A can be shown to depend on the specific values in M. This is easy to show for a 2*2 matrix.

Another way to see that is that matrix representation would be n² by n², the dimension of the space of n x n matrices. The sizes don't match. Flattening M is equivalent to finding a coordinate vector for M with respect to some basis of the space of matrices, so the vector will have n² components. and everything works out.

 

[lpetrich]

Find the eigenvalues and eigenvectors of these matrices:

Rotation:
\(\begin{bmatrix} \cos a & - \sin a \\ \sin a & \cos a \end{bmatrix}\)

Rotation and reflection:
\(\begin{bmatrix} \cos a & \sin a \\ \sin a & - \cos a \end{bmatrix}\)

Boost:
\(\begin{bmatrix} \cosh u & \sinh u \\ \sinh u & \cosh u \end{bmatrix}\)

Boost and reflection 1:
\(\begin{bmatrix} \cosh u & - \sinh u \\ \sinh u & - \cosh u \end{bmatrix}\)

Boost and reflection 2:
\(\begin{bmatrix} - \cosh u & - \sinh u \\ \sinh u & \cosh u \end{bmatrix}\)

Boost and reflections 1 and 2
\(\begin{bmatrix} - \cosh u & \sinh u \\ \sinh u & - \cosh u \end{bmatrix}\)

Any patterns in them?

 

[steve_bnk]

Eigenvalues I understand. Rotation and reflection of a matrix is too theoretical for me, I'd have to look it up. Don't see anything about boost.

http://en.wikipedia.org/wiki/Rotation_matrix

Looks like it applies to graphics.

in physical systems the eigenvalues represent physical resonances. what do the eigenvalues mean in the problem.

The eigenvalues are the solutions to the matrix characteristic equation. A 2x2 matrix yields a quadratic.

 

[steve_bnk]

1. How many ways are there to make change of $1, using pennies, nickels, dimes, and quarters?
2. What is the optimal set of four coin denominations? (i.e. we are allowed 4 different denominations and want to minimize the average number of coins necessary to make change for any value from 1c to 99c, each equally likely)
3. If you repeatedly play a game where you can randomly win either $3 or $7, what is the largest dollar amount that it is not possible for you to cumulatively win? What about other $a and $b?

What is your solution for #3

 

[barbos]

Quantum mechanics is actually not different than basic engineering principles.

and then this

Eigenvalues I understand. Rotation and reflection of a matrix is too theoretical for me, I'd have to look it up. Don't see anything about boost.

http://en.wikipedia.org/wiki/Rotation_matrix

Looks like it applies to graphics.

in physical systems the eigenvalues represent physical resonances. what do the eigenvalues mean in the problem.

The eigenvalues are the solutions to the matrix characteristic equation. A 2x2 matrix yields a quadratic.

 

[steve_bnk]

and then this

Eigenvalues I understand. Rotation and reflection of a matrix is too theoretical for me, I'd have to look it up. Don't see anything about boost.

http://en.wikipedia.org/wiki/Rotation_matrix

Looks like it applies to graphics.

in physical systems the eigenvalues represent physical resonances. what do the eigenvalues mean in the problem.

The eigenvalues are the solutions to the matrix characteristic equation. A 2x2 matrix yields a quadratic.

And this what? Be specific if you are making a critique. I make no claim to be a theoretical master of anything in math. I do know ad use the application of linear algebra in engineering.

Resonance represented by eigenvalues of sets of system equations are common across Newtonian mechanics, quantum mechanics, control systems, and electrical theory.

 

[steve_bnk]

a = 4
b = d * (1/n)
c = a – b
d = c * m

m = 100
n = 10


Solve for the expression d/a =

What is the value of d?

In the limit as m -> inf what is d?

 

[bigfield]

a = 4
b = d * n
c = a – b
d = c * m

m = 100
n = 10

What is the value of d?

c = a - b
c = a - d * n
c = a - c * m * n
a = c + c * m * n
a = c(1 + m * n)
c = a/(1 + m * n)

d = c * m
d = ma/(1 + m * n)
d = (100 * 4)/(1 + 100 * 10)
d = 400/1001

 

[lpetrich]

I'll do the eigenvalues and eigenvectors of those matrices. In general, a matrix M can be decomposed into matrices D and V satisfying
M.V = V.D

In general, D is in Jordan normal or canonical form, a matrix where only the main diagonal and its neighboring upper right diagonal may have nonzero elements. The main-diagonal elements of D are M's eigenvalues and D's off-main-diagonal elements are either 0 or 1. V is a matrix of generalized right eigenvectors. Its transpose of its inverse is a matrix of generalized left eigenvectors.

Rotation R:
\( M = \begin{bmatrix} \cos a & - \sin a \\ \sin a & \cos a \end{bmatrix} ,\ D = \text{diag}(e^{ia},e^{-ia}) ,\ V = \begin{bmatrix} 1 & 1 \\ -i & i \end{bmatrix} \)

Rotation and reflection RR:
\( M = \begin{bmatrix} \cos a & \sin a \\ \sin a & - \cos a \end{bmatrix} ,\ D = \text{diag}(1,-1) ,\ V = \begin{bmatrix} \cos a/2 & - \sin a/2 \\ \sin a/2 & \cos a/2 \end{bmatrix} \)

Boost B:
\( M = \begin{bmatrix} \cosh u & \sinh u \\ \sinh u & \cosh u \end{bmatrix} ,\ D = \text{diag}(e^{u},e^{-u}) ,\ V = \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \)

Boost and reflection 1 BR1:
\( M = \begin{bmatrix} \cosh u & - \sinh u \\ \sinh u & - \cosh u \end{bmatrix} ,\ D = \text{diag}(1,-1) ,\ V = \begin{bmatrix} \cosh u/2 & \sinh u/2 \\ \sinh u/2 & \cosh u/2 \end{bmatrix} \)

Boost and reflection 2 BR2:
\( M = \begin{bmatrix} - \cosh u & - \sinh u \\ \sinh u & \cosh u \end{bmatrix} ,\ D = \text{diag}(1,-1) ,\ V = \begin{bmatrix} - \sinh u/2 & \cosh u/2 \\ \cosh u/2 & - \sinh u/2 \end{bmatrix} \)

Boost and reflections 1 and 2 BR12:
\( M = \begin{bmatrix} - \cosh u & \sinh u \\ \sinh u & - \cosh u \end{bmatrix} ,\ D = \text{diag}(-e^{u},-e^{-u}) ,\ V = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \)

See any patterns?

Here's another challenge associated with them. Consider generalizing the inner product of two vectors:
a quadratic form (x,y) = x.g.y where g is real and symmetric.

If for some M, (M.x,M.y) = (x,y) is true for all x and y, then M is an isometry or a symmetry transformation of that quadratic form, and it satisfies
M^T.g.M = g

What g's satisfy this equation for matrices R, RR, B, BR1, BR2, and BR12?

 

[lpetrich]

Here are the solutions for the metric g for the various matrices.
R, RR: g = diag(1,1) -- Euclidean metric
B, BR1, BR2, BR12: g = diag(1,-1) -- Lorentzian metric

Note a connection with special relativity. Start with matrix B, set u = arctanh(v/c) for velocity v, and having it operate on vector {x, c*t}. One gets the Lorentz transformations or boosts. In general, transformations on space-time directions fall into 4 categories of connected one:
Pure rotations and boosts and combinations of them
R's and B's with space reflection
R's and B's with time reflection
R's and B's with both space and time reflections

This is the Lorentz group, O(3,1), and R's and B's are the restricted Lorentz group, SO⁺(3,1) or sometimes plain SO(3,1).

But for a Euclidean metric, like for 2-space and 3-space, there are only 2 connected categories: pure rotations and rotation-reflections. Those one's groups are O(2) and O(3) with pure rotations being SO(2) and SO(3).

 

[lpetrich]

I'll now consider more general properties of rotation/reflection matrices.

They are real and orthogonal: for matrix R, R^T.R = I, the identity matrix. That will tell us something about their eigenvalues and eigenvectors:
R.x = r*x

Since det(R)² = 1, det(R) = 1 (pure rotations) or -1 (rotations + reflections). Note that det(R) = product of all its r's.

Consider x^*.R.x where the * means complex conjugate. It is
x^*.R.x = r*(x^*.x) = (r^*)sup]-1[/sup]*(x^*.x)

Since (x^*.x) > 0 unless x is identically zero, r must have |r| = 1. So the r values are 1's, -1's, and pairs of complex conjugates for nonzero imaginary part.

Challenge: How many 1's and -1's are in the eigenvalues of a pure rotation matrix? In those of a rotation-reflection matrix? How may the eigenvalues and eigenvectors be interpreted as rotations and reflections?

 

[steve_bnk]

d/a = 1/( (1/M(f)) + N(f)) where M and N are functions of frequency.

The basic negative feedback control equation. As M gets large system behavior is dominated by N the feedback function a desirable condition.

With M being high, N can be configured to perform mathematical operations like integration, addition, and subtraction. hence the adoption of the term 'operational amplifier' during WWII. Analog electronic computation ad analog computers used to solve differential equations.

The eigenvalues of the denominator determine system behavior.

 

[lpetrich]

Oops, that's
x^*.R.x = r * (x^*.x) = (r^*)^-1 * (x^*.x)

So a real orthogonal matrix has these possible eigenvalues: 1, -1, and a pair of e^i*a and e^-i*a.

Eigenvalue 1 means identity: R.x = x
Eigenvalue -1 means inversion: R.x = -x
The pairs have a more complicated meaning. Let e^i*a have eigenvalue x = x1 + i*x2 where x1 and x2 are real vectors. Then,
e^-i*a has eigenvalue x^* = x1 - i*x2
and
R.x = e^i*a * x
can be expanded into its real and imaginary parts, giving
R.x1 = x1*cos(a) - x2*sin(a)
R.x2 = x1*sin(a) + x2*cos(a)

Also,
x.R.x = e^i*a * (x.x) = e^-i*a * (x.x)
For sin(a) != 0,
x2.x2 = x1.x1 and x1.x2 = 0

Thus, eigenvalue pair e^i*a and e^-i*a correspond to a 2D rotation. Two identities are for a = 0, and two inversions for a = π.

Thus, the eigenvalues of a rotation matrix are pairs corresponding to 2D rotations with either none or one of both 1 and -1, identity and inversion.

The determinant of a matrix is the product of its eigenvalues, so a pure rotation matrix has an even number of -1's and a rotation-reflection matrix an odd number.

Here's a table:
[table="class: grid"]
[tr]
[td]# Dims[/td]
[td]Rot/Refl[/td]
[td]Extra e's[/td]
[/tr]
[tr]
[td]Even[/td]
[td]Rot: 1[/td]
[td][/td]
[/tr]
[tr]
[td]Even[/td]
[td]Refl: -1[/td]
[td]1, -1[/td]
[/tr]
[tr]
[td]Odd[/td]
[td]Rot: 1[/td]
[td]1[/td]
[/tr]
[tr]
[td]Odd:[/td]
[td]Refl: -1[/td]
[td]-1[/td]
[/tr]
[/table]

 

[lpetrich]

I'll now consider the pseudo-orthogonal case, where R^T.g.R = g for symmetric g and g = g^-1 for convenience.

x^*.R.x = r * (x^*.x)
But
x^*.R.x = x.R^T.x^* = (g.x).R^-1.(g.x^*)

Thus, (g.x^*) has eigenvalue r^-1 and (g.x) eigenvalue r^*-1.

Considering x^*.g.R.x gives us (r^*-1 - r) * (x^*.g.x) = 0
Also, x.R.x gives us (r^* - r) * (x.x) = 0
and x.g.R.x gives us (r^-1 - r) * (x.g.x) = 0


Let's see what eigenvalues R can have.

If r has values 1 (identity) or -1 (inversion), then x can be real and both (x.x) and (x.g.x) can be nonzero. Each such r is associated with no others.

If r is different from 1 and -1, then r^-1 != r and (x.g.x) = 0

If r is real, then x can be real and (x.x) must then be nonzero. The eigenvalue r occurs in a pair, {r, r^-1} with eigenvectors {x, g.x}. It is thus like a Lorentz boost.

Thus x must be nonzero on both the + side and the - side of g. That is, splitting x into x₊ (the plus side) and x_- (the minus side), with g.x₊ = x₊ and g.x_- = - x_-. Both x₊ and x_- must be nonzero.

If r is non-real complex, then (x.x) must be zero. Their are now four possible eigenvalues, {r, r^*, r^-1, r^*-1}, corresponding to eigenvectors {x, x^*, g.x^*, g.x}.

This case reduces to a two-eigenvalue case, {r, r^*} with eigenvectors {x, x^*}, if |r| = 1. Then x and (g.x) share eigenvalue r. Take y1 = x + (g.x) and y2 = x - (g.x). Then g.y1 = y1 and g.y2 = -y2, and by selecting either y1 or y2 as the eigenvector, g.(it) is proportional to it, and thus not a distinct eigenvector.

In this case, x must be nonzero only on the + side or the - side of g, not on both sides. It thus represents a 2D rotation.

In the case of four related eigenvalues, (x.x) = (x.g.x) = 0, thus making (x<sub>+[/sup].x⁺) = (x-.x-) = 0, with x+ being the part of x on the + side of g and x- being the part on the - side. Since x and g.x are distinct eigenvectors, both x+ and x- must be nonzero. They are therefore complex, with x+r.x+r = x+i.x+i and x+r.x+i (r and i are the real and imaginary parts), and likewise for x-.

This means that an eigenvalue quadruplet can only happen when there is more than one dimension on each side of g, more than one dimension on the + side and more than one dimension on the - side. Thus, for space-time and its Lorentz group of rotations, boosts, and reflections, the eigenvalues are 1, -1, real, or magnitude-1 complex. They cannot be complex with non-unity magnitude.</sub>

 

[steve_bnk]

Must be strange to lecture to an empty hall.

 

[Kharakov]

The following infinite series is created by manipulating a form of the Taylor series for \(\sqrt[n]{x^n-b}\). It is only part of the series- it excludes the first term, and the signs are the opposite of the original series.

\( \frac {1}{n \times 1!} - \frac {1-n}{n^2 \times 2!} +\frac {(1-n) (1-2n)}{n^3 \times 3!} - \frac {(1-n) (1-2n) (1-3n)}{n^4 \times 4!} ...\)

What does it equal?

hint:

Show

There's a pretty easy way to produce part of Pascal's triangle with the series

Show

input 1/positive integer

There is also an inflection point which causes the series to approach one way, or the other to the value.

 

[beero1000]

The following infinite series is created by manipulating a form of the Taylor series for \(\sqrt[n]{x^n-b}\). It is only part of the series- it excludes the first term, and the signs are the opposite of the original series.

\( \frac {1}{n \times 1!} - \frac {1-n}{n^2 \times 2!} +\frac {(1-n) (1-2n)}{n^3 \times 3!} - \frac {(1-n) (1-2n) (1-3n)}{n^4 \times 4!} ...\)

What does it equal?

hint:

Show

There's a pretty easy way to produce part of Pascal's triangle with the series

Show

input 1/positive integer

There is also an inflection point which causes the series to approach one way, or the other to the value.

I like it. There's no need to bring up the Taylor series of \(\sqrt[n]{x^n-b}\) though, the binomial theorem is sufficient.

 

[Kharakov]

The following infinite series is created by manipulating a form of the Taylor series for \(\sqrt[n]{x^n-b}\). It is only part of the series- it excludes the first term, and the signs are the opposite of the original series.

\( \frac {1}{n \times 1!} - \frac {1-n}{n^2 \times 2!} +\frac {(1-n) (1-2n)}{n^3 \times 3!} - \frac {(1-n) (1-2n) (1-3n)}{n^4 \times 4!} ...\)

What does it equal?

hint:

Show

There's a pretty easy way to produce part of Pascal's triangle with the series

Show

input 1/positive integer

There is also an inflection point which causes the series to approach one way, or the other to the value.

I like it. There's no need to bring up the Taylor series of \(\sqrt[n]{x^n-b}\) though, the binomial theorem is sufficient.

I didn't think of that.

 

[lpetrich]

The following infinite series is created by manipulating a form of the Taylor series for \(\sqrt[n]{x^n-b}\). It is only part of the series- it excludes the first term, and the signs are the opposite of the original series.

\( \frac {1}{n \times 1!} - \frac {1-n}{n^2 \times 2!} +\frac {(1-n) (1-2n)}{n^3 \times 3!} - \frac {(1-n) (1-2n) (1-3n)}{n^4 \times 4!} ...\)

What does it equal?

In general,
\( (1 + x)^p = 1 + \frac{p}{1!} x + \frac{p(p-1)}{2!} x^2 + \frac{p(p-1)(p-2)}{3!} x^3 + \cdots \)
The general term is
\( p(p-1) \cdots (p-k+1) \frac{x^k}{k!} \)

Calling Kharakov's quantity K, it is equal to \( 1 - (1+x)^p \) where p = 1/n and x = -1. Thus, for n > 0, K = 1.

 

[Kharakov]

That works too. My route was more complicated.

I arrived at it by doing the Taylor series for \((x^n-b)^{(1/n)}\) with b= x^n. When you do that you end up with:

x - x*first term + x*second term - x*third term.... dividing through by x you get:

1 - first term + second term - third term +....

and since the Taylor series adds up to 0 (for x^n-x^n), and the first term is 1, the rest of the terms = -1. So I flopped the signs on the rest, and got 1.

If you want to make arriving at 1 complicated, use my route.