Beware, there be math below...
We need to be careful with our assumptions here. There are potential flat, finite, and static universes that are possible that don't have any 'edges'.
There are 18 candidate topologies for flat universes without edges (the number of Euclidean 3-manifolds) and we don't really know which one we live in. Of the 18, eight are non-orientable. While it's possible the universe is non-orientable that would have super weird consequences that we don't see in our universe (we've checked).
So there are 10 candidate orientable Euclidean 3-manifolds. Of these, 4 are non-compact (essentially, infinite in at least one direction) and 6 are compact (essentially, finite in every direction). I'm going to try and describe them, but they are a challenging exercise in 3D visualization and I'm too lazy to post figures, so bear with me.
The 4 non-compact, orientable, Euclidean 3-manifolds are:
- \(\mathbb{R}^3\). This is our intuitive, standard, 3D Euclidean space.
- \(\mathbb{R}^2 \times S^1\). This is the 3D analog of a cylinder
- \(\mathbb{R} \times S^1 \times S^1\). This space has one 'normal' infinite dimension while the other two form Pac-man's space (a torus)
- The easiest way to describe this space is as the previous one but with a half twist (e.g. Pac-man goes through one side and comes out the other, not directly across but rather flipped about the infinite axis.
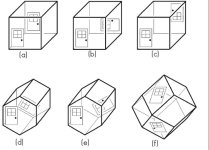
The 6 compact, orientable, Euclidean 3-manifolds are:
- \(S^1 \times S^1 \times S^1\). This is the 3-torus, the 3D analog of Pac-man space.
- 3D Pac-man space but with a quarter twist of one dimension (e.g. you go through that square wall and come out on the opposite wall rotated 90 degrees).
- 3D Pac-man space but with a half twist of one dimension.
- Think of this one as 3D Pac-man, but where one pair of walls is split in two and you teleport diagonally across the split pairs.
- Think of this one as 3D Pac-man on a hexagonal prism, but with a 1/6 twist in the hexagonal dimension.
- Think of this one as 3D Pac-man on a hexagonal prism, but with a 1/3 twist in the hexagonal dimension.
From what I understand, most cosmologists think that we live in one of the latter 6 (the compact, orientable, Euclidean 3-manifolds). But which? We don't currently know, but studies in cosmic microwave background might find out in the future.
To answer your question about jumping off a trampoline, it would depend on the shape of the universe and the direction you were jumping. Pick and we can work through what would happen...