NASA engineers

[Peez]

steve_bnk:
I did not see it, with my yes I sometimes click on the wrong selection from the spell checker.

I guessed that spell-checker was to blame. It is only a question of time before a war gets started by that mechanism.

Peez

 

[Peez]

Emily Lake:
I don't see why you think this is a husband beating situation. I think it was a valid question, please allow me to elaborate.

The reason that I was unhappy with the question was that you seemed to be asking: "If you shouldn't report the variance, would you report the variance?" Since I have tried to make it clear that I do not think that reporting variability in these situations is a problem, then the question seemed silly to me.

Yes, your case is true, if the sample size is large enough to be reasonable and the distribution is normal.

It does not have to be normal (Gaussian), though with the Central Limit Theorem we suspect that the distribution of means is. In any event the variance is informative whether or not the variable is normally distributed, even if the variance might not have the familiar specific relationship with non-normal distributions.

Then reporting mean and variance allows the reader to make some estimate of whether the sample is credible.

Just to be clear, when you state "whether the sample is credible" I presume that you mean approximately 'whether statistics calculated from the sample are useful', is that a fair rephrasing?

I think, however, that there is a difference that should be considered when the sample size is small. I'm getting into things that I can envision, but I may not be articulating well. Some of the stuff I work with is in trying to determine whether or not a correlation exists - whether there is a distribution at all, or whether it is random.

By "random" here, would it be fair to presume that you mean 'one variable is uncorrelated with the other'? I am sorry to be pedantic, I just want to avoid any misunderstanding.

With a small sample, I can calculate mean and variance, sure. But if I get a high variance, I can't necessarily tell if the small sample I have contains a legitimate low probability tail measurement, or if it is random and indicative of low correlation. If I report the mean and variance in a small sample, someone in my not-so-informed audience is going to assume that because I've reported statistical measures, that the results must therefore be robust and credible. Simply the fact that I've reported statistics means that statistics are credible to that audience.

Ah, perhaps this is where we are not understanding each other. I agree that people generally do not understand statistics (there is an understatement for you), as with any topic it might be wise to simplify things to avoid confusion. Not not everyone agrees, but I understand the sentiment. Would you agree that a variance can be calculated from a sample with five data points, and that one should include an estimate of variability whenever reporting a mean to an audience of colleagues?

You as an actual statistician might have more sense... but they don't, and I think that many readers don't.

I am not a statistician, I am just a biologist who has used statistics quite a bit, but I agree that many people (even many people who should) do not really understand statistics.

I try very hard to never imply more credibility or certainty than I actually have. There've been times where my caveats are longer than my material!

That is a sign of wisdom. I should probably include more! Thank you for your detailed post.

That was the basis of my question. How would you advise your students for situations like that? I'm genuinely curious what your take is on it.

I would advise my students to never report a mean without an estimate of variability in the data (and a sample size). I would also advise them to obtain a sample size greater than five, if they can. If they were to present results to a 'lay' audience, I would suggest explaining to that audience the limitations of the statistics (something that they should do in any event, even with large sample sizes and robust statistics such an audience can get the wrong ideas).

In regard to having failed to address your point, I'm sorry. I'm not entirely sure what point you feel I missed. If you tell me again, I'll endeavor to address it.

Fair enough. I was hoping that you could comment on the importance of knowing the variance from the sample you offered as an example, in contrast to the alternate sample that I presented (that had the same mean).

Peez

 

[barbos]

here is distribution of standard deviation of N=5 sets.
As you can see N=5 SD is within 30% of actual SD.
So 5 measurements is good enough for estimation errors.

 

[steve_bnk]

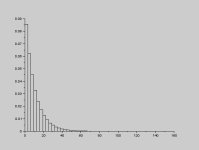
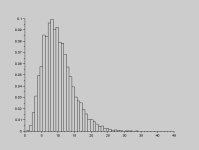
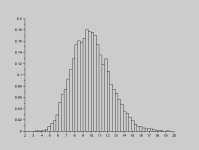
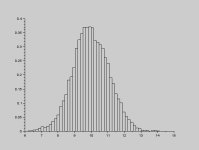
View attachment 857

here is distribution of standard deviation of N=5 sets.
As you can see N=5 SD is within 30% of actual SD.
So 5 measurements is good enough for estimation errors.

M
Maybe it is a language problem. I do not see what you are trying to represet.

What I see is a normal PDF with mean 1 and standard deviation of 0.33.

In terms of the op (irony) detail what you are trying to prove and the exact process you took.

30/ is not 'good enough', it all dpends on what the situaio requires.

 

[barbos]

Couple of people here claimed that 5 measurements is not enough to estimate standard deviation of the distribution.
Histrogram I posted is a proof that 5 measurements is good enough.
It's effectively error of the error.
It shows distribution of SD calculated using 5 measurements. It shows that 60% of time SD calculated using only 5 measurements will be within 30% of true value.
In any case, this was a ridiculous excuse for lack of errors in the lab report.
And not only ridiculous but false too.

 

[steve_bnk]

Couple of people here claimed that 5 measurements is not enough to estimate standard deviation of the distribution.
Histrogram I posted is a proof that 5 measurements is good enough.
It shows distribution of SD calculated using 5 measurements. It shows that 60% of time SD calculated using only 5 measurements will be within 30% of true value.

Yes you can estimate mean and sd from a sample of 5, that is not the question.

The question is the usefulness of an estimate from such a small sample. If I needed to know the mean and sd of a dimension of a mechanical part for design purposes of which I had several thousand a sample size of 5 and a 30% error would likely be unacceptable.

If you only have 5 samples then you are stuck with it.

If you have a population to sample from the task is to design a sampling plan that meets a confidence level requirement.

My first major project way back in the 80s was setting a field failure and manufacturing statistical analysis system.

Restating what someone posted. Taking a class in statistics is not the same as knowing how to apply it in the real world to solve a problem..

Statistical parameters have meaning only in some context in which they are applied. if you can live with a 30% uncertainty, then you achieved your goal.

 

[barbos]

Couple of people here claimed that 5 measurements is not enough to estimate standard deviation of the distribution.
Histrogram I posted is a proof that 5 measurements is good enough.
It shows distribution of SD calculated using 5 measurements. It shows that 60% of time SD calculated using only 5 measurements will be within 30% of true value.

Yes you can estimate mean and sd from a sample of 5, that is not the question.

The question is the usefulness of an estimate from such a small sample. If I needed to know the mean and sd of a dimension of a mechanical part for design purposes of which I had several thousand a sample size of 5 and a 30% error would likely be unacceptable.

If you only have 5 samples then you are stuck with it.

If you have a population to sample from the task is to design a sampling plan that meets a confidence level requirement.

My first major project way back in the 80s was setting a field failure and manufacturing statistical analysis system.

Restating what someone posted. Taking a class in statistics is not the same as knowing how to apply it in the real world to solve a problem..

Statistical parameters have meaning only in some context in which they are applied. if you can live with a 30% uncertainty, then you achieved your goal.

Unless you have an actual objections to my actual proof, I suggest to shove it.
You are in no position to posture me about practical statistics. As someone who has PhD in the field where you spend half of the time doing exactly that, I have more practical experience than all people here combined.

30% error is on error, not on the measurement, it is almost always enough, and certainly better than no error at all.
The fact is, presenting a measurement without uncertainty is unheard of in hard science such as physics.

 

[steve_bnk]

Yes you can estimate mean and sd from a sample of 5, that is not the question.

The question is the usefulness of an estimate from such a small sample. If I needed to know the mean and sd of a dimension of a mechanical part for design purposes of which I had several thousand a sample size of 5 and a 30% error would likely be unacceptable.

If you only have 5 samples then you are stuck with it.

If you have a population to sample from the task is to design a sampling plan that meets a confidence level requirement.

My first major project way back in the 80s was setting a field failure and manufacturing statistical analysis system.

Restating what someone posted. Taking a class in statistics is not the same as knowing how to apply it in the real world to solve a problem..

Statistical parameters have meaning only in some context in which they are applied. if you can live with a 30% uncertainty, then you achieved your goal.

Unless you have an actual objections to my actual proof, I suggest to shove it.
You are in no position to posture me about practical statistics. As someone who has PhD in the field where you spend half of the time doing exactly that, I have more practical experience than all people here combined.

30% error is on error, not on the measurement, it is almost always enough, and certainly better than no error at all.
The fact is, presenting a measurement without uncertainty is unheard of in hard science such as physics.

Resort to academic credentials, the last resort. First you said you had a course, now you say you are a PHD in statistics? The math of statistics is is not difficult. I spent several years in the 80s going through the books and coding algorithms on my first PC.

I am not a PHD, I am autodidactic always exploring and self learning. Classes to me were always slow and tortuous. I am not dismissive of advanced degrees, but for me a PHD carries no special weight. Armed with undergrad math and science one can teach oneself and apply most anything.

What is the definition of a probability distribution and how would you determine the first and second moments?

You must have a reading comprehension problem. As I said yes you can compute mean and sd from a sample of 5, and that is not the issue.

What you did was tautological. SD is a definition, it can not be proven it is.

There is a population or true mean and SD, and there are sample means and sample SD as estimates to the true population values.. The question is how close your sample statistics need to be to the population parameter in a specific case. Do you understand this statement? There is no 30% is usually good enough. The assertion is rather silly.

We are not talking about measurement errors per se. We are talking about sampling in this case from a normal PDF population. Statistically measurements are essentially a sampling process from a distribution.

I've spent 30 years applying science, engineering, and math to real world situations. Again, 30% good enough for what? Give some examples. You have no basis or such a generalization.

Here is a typical real world problem. I have a box of 10,000 resistors said to be nominally 1000 ohms.. I need to know the mean and the 6 sigma bounds on resistance values for design tolerancing.

How would you analytically set sample size to know the mean resistance value to a confidence level of 90%. Sampling with or without replacement?

What do you do with an exponential distribution that models electronic systems reliability?

I suggest Duncan's Quality Control And Industrial Statistics. An older publication but the best general book I've seen on applied statistics. Lost my copy.

 

[Emily Lake]

It does not have to be normal (Gaussian), though with the Central Limit Theorem we suspect that the distribution of means is. In any event the variance is informative whether or not the variable is normally distributed, even if the variance might not have the familiar specific relationship with non-normal distributions.

My error, that should have read "if the sample size is large enough OR the distribution is normal (yes, gaussian) )

Just to be clear, when you state "whether the sample is credible" I presume that you mean approximately 'whether statistics calculated from the sample are useful', is that a fair rephrasing?

I suppose I mean more that statistics are meaningful. In my line of work, useful and meaningful aren't always the same thing. I work with a lot of models where anything over a 0.5 r-squared is considered an excellent fit! It's a lot of really qualitative and directional survey stuff, and the models aren't maybe as accurate as one would like to see in many other fields. Sometimes we work with stuff that is useful because it's the best we've got... knowing full well that it's not particularly meaningful, and the error in the model just keeps growing and growing. It kind of depends on the application, and what kind of question we're trying to answer. It may not have much utility to you... but I end up keeping different classes for useful, meaningful, and material. They're not the same things to me. Useful means that it suggests a relationship, but one can't be shown to exist because we don't have enough data, or the stats aren't significant. Meaningful means that there's enough data to do some tests that will let us actually test a hypothesis, and reject the null in some cases (or fail to), and draw meaningful conclusions about the sample, but that the magnitude may not be quantifiable or the magnitude is quantifiable but small relative to the measurement we're interested in. Material means it is meaningful AND it is quantifiable and not negligible relative to our measurement of interest. There's some gray area involved depending on the project and the nature of the question at hand, of course.

By "random" here, would it be fair to presume that you mean 'one variable is uncorrelated with the other'? I am sorry to be pedantic, I just want to avoid any misunderstanding.

Yes. Did I mention that I'm re-learning a lot of the stuff I've forgotten?

Would you agree that a variance can be calculated from a sample with five data points, and that one should include an estimate of variability whenever reporting a mean to an audience of colleagues?

I suppose. I can see the sense in it, at least. I can tell you that I don't necessarily do so, and maybe that's just poor practice, but it's pragmatic. For example, one of the things I do is put together some models that look at both prevalence and severity for several diagnoses and procedures. We're working with a really huge data set - on the order of 5 million patients, and tens of millions of events. I've got thirty different diagnosis/procedure elements going in to this model, and I'm calculating prevalence and severity separately across five different input variables, to come up with compound estimates for each element, then aggregating them all for a total impact analysis. I could calculate variance for each of those elements and take it into consideration... but it's immaterial to the final output of this model. Central Limit Theorem dominates the outcome well enough that the variances involved end up being chaff when compared to the uncertainties that get layered on top of that model. At the end of the day, the effort involved in calculating the variances and properly combining them is irrelevant to the questions being asked... it would take more time than those variance would add with actual real value in terms of knowledge gained. So I don't do it. But I understand your point

Fair enough. I was hoping that you could comment on the importance of knowing the variance from the sample you offered as an example, in contrast to the alternate sample that I presented (that had the same mean).

Peez

Ah. Yes, I see what you mean. Yes, there is value in reporting that SD from that perspective.

In the context of the work done by NASA, what is your opinion of how they reported their results? In this case, a sample of 5 was the largest of their samples - most of them were only 1 or 2. They didn't calculate variance, but they did report the range of measurements when there were more than one taken.

To barbos' complaint, upon further thought, I'm not certain they could have calculated error in any case. I previously said that error is a function of variance, which is true... and stipulated that there were too few measurements to calculate variance with any statistical credibility. Upon further reflection and thought, however, I realize that I was incorrect - to calculate error, you must have an expectation. It is my impression that NASA could not have had a calculated expected value for their measurements... since by all accounts it shouldn't work at all! And without an expected value, you can't calculate error from expected, right?

Or am I wrong?

 

[steve_bnk]

The Central Limit Theorem is linked to the Law Of Large Numbers.

http://en.wikipedia.org/wiki/Law_of_large_numbers



An exponential distribution mean = 10.




As the sample size gets large the distribution of sample means is approximated by a normal PDF.


Distribution of sample means, sample size = 5.




Distribution of sample means, sample size = 20




Distribution of sample means, sample size = 80.




At a sample size of 80 the distribution of sample means looks normal.

 

[beero1000]

To barbos' complaint, upon further thought, I'm not certain they could have calculated error in any case. I previously said that error is a function of variance, which is true... and stipulated that there were too few measurements to calculate variance with any statistical credibility. Upon further reflection and thought, however, I realize that I was incorrect - to calculate error, you must have an expectation. It is my impression that NASA could not have had a calculated expected value for their measurements... since by all accounts it shouldn't work at all! And without an expected value, you can't calculate error from expected, right?

Or am I wrong?

Different meanings of 'error'. Barbos is talking about the standard error of the sampling distribution of the sample variance. With standard assumptions, the scaled sampling distribution will be chi-square (his is actually (mostly) a chi-distribution due to graphing SD instead of variance - yuck ). You'd then use the variance of the variance to estimate how off your sample variance could be.

Nothing super controversial here, all this should be taught in most intro statistics courses (except maybe the ones for English majors ). At least, it was when I taught it in a 100 level course a few years ago.

 

[barbos]

Unless you have an actual objections to my actual proof, I suggest to shove it.
You are in no position to posture me about practical statistics. As someone who has PhD in the field where you spend half of the time doing exactly that, I have more practical experience than all people here combined.

30% error is on error, not on the measurement, it is almost always enough, and certainly better than no error at all.
The fact is, presenting a measurement without uncertainty is unheard of in hard science such as physics.

Resort to academic credentials, the last resort.

Really? And how about your resorting to years of experience?

First you said you had a course, now you say you are a PHD in statistics?

Nope, that's not what I said, You seem to be having reading comprehension problems.

The math of statistics is is not difficult. I spent several years in the 80s going through the books and coding algorithms on my first PC.

Resorting to your experience again?

I am not a PHD, I am autodidactic always exploring and self learning. Classes to me were always slow and tortuous. I am not dismissive of advanced degrees, but for me a PHD carries no special weight. Armed with undergrad math and science one can teach oneself and apply most anything.

I don't have a slightest interest in your life experiences, sorry.

---
more posturing and lecturing
---

I see nothing to comment here, so I just repeat again.

5 measurement is enough to estimate standard deviation and is done all the time. Everybody who has gone through undergraduate physics lab knows and literally has done it (estimating errors based on 5 measurements)

 

[steve_bnk]

Resort to academic credentials, the last resort.

Really? And how about your resorting to years of experience?

First you said you had a course, now you say you are a PHD in statistics?

Nope, that's not what I said, You seem to be having reading comprehension problems.

The math of statistics is is not difficult. I spent several years in the 80s going through the books and coding algorithms on my first PC.

Resorting to your experience again?

I am not a PHD, I am autodidactic always exploring and self learning. Classes to me were always slow and tortuous. I am not dismissive of advanced degrees, but for me a PHD carries no special weight. Armed with undergrad math and science one can teach oneself and apply most anything.

I don't have a slightest interest in your life experiences, sorry.

---
more posturing and lecturing
---

I see nothing to comment here, so I just repeat again.

5 measurement is enough to estimate standard deviation and is done all the time. Everybody who has gone through undergraduate physics lab knows and literally has done it (estimating errors based on 5 measurements)

Yes, taking a few measurements and averaging is common. The SD gives you an idea of variability.

You are unable to support your 'good enough 'claim other than they do it in physics 101 labs?.

But again, how do you determine a sample size to meet a confidence level requirement? Do you even understand the question yes or no?.

It is covered in any basic text.

Taking a few measurements and averaging is descriptive.

Determining how you will sample to meet a measurement accuracy objective is not the same thing, as I determining the number of test runs in the OP paper.

You do not appear to understand the difference.

I receive a large crate of 1000 metal rods and I want to check against mean length specification. If I install them in a product and they are out of spec there will be financial issues. Would you just use 5 samples without thinking.? Another yes no question.

Resorting to my experience? Both experience and theory. herylone ledsto dangerous decisions. I refuted you with simple examples.

I like to use 20 as a min sample based on experience and theory. As N gets large normal statistics becomes a good approximation for parameters,.

I showed in my last post that when random sampling from an exponential distribution as N increases the distribution of sample means become normal, the CLT. A desirable condition.

http://en.wikipedia.org/wiki/Sample_size


When measuring a deterministic electrical signal corrupted by random noise we average measurements. The +- deviations about the mean average to zero. In the limit as n gets large the average approaches the true value of the signal, Law Of large Numbers.

 

[Peez]

Emily Lake:
I suppose I mean more that statistics are meaningful. In my line of work, useful and meaningful aren't always the same thing. I work with a lot of models where anything over a 0.5 r-squared is considered an excellent fit! It's a lot of really qualitative and directional survey stuff, and the models aren't maybe as accurate as one would like to see in many other fields. Sometimes we work with stuff that is useful because it's the best we've got... knowing full well that it's not particularly meaningful, and the error in the model just keeps growing and growing. It kind of depends on the application, and what kind of question we're trying to answer. It may not have much utility to you... but I end up keeping different classes for useful, meaningful, and material. They're not the same things to me. Useful means that it suggests a relationship, but one can't be shown to exist because we don't have enough data, or the stats aren't significant. Meaningful means that there's enough data to do some tests that will let us actually test a hypothesis, and reject the null in some cases (or fail to), and draw meaningful conclusions about the sample, but that the magnitude may not be quantifiable or the magnitude is quantifiable but small relative to the measurement we're interested in. Material means it is meaningful AND it is quantifiable and not negligible relative to our measurement of interest. There's some gray area involved depending on the project and the nature of the question at hand, of course.

This touches on an important point that can be lost when one is immersed in statistics: it is important to distinguish between statistical significance and experimental significance (for lack of a better term). Just because a result is found to be formally "statistically significant" does not automatically mean that the result is significant to the phenomenon that one is studying.

In the context of the work done by NASA, what is your opinion of how they reported their results? In this case, a sample of 5 was the largest of their samples - most of them were only 1 or 2. They didn't calculate variance, but they did report the range of measurements when there were more than one taken.

I mostly skimmed the article, much of the technical aspects are beyond my understanding, but I did not see any reason that the sample sizes were so low and so my first thought (apart from adjusting to the use of English measurements in a published paper) was that they should have completed more replicates. Another issue that I noticed was statements such as "Based upon this observation, both test articles (slotted and unslotted) produced significant thrust in both orientations (forward and reverse)." without any basis for determining that the results were significant (statistically or experimentally).

That being said, Table 1 does present ranges, which one might argue to be appropriate in this case (given the sample sizes). An argument might be made to report SD, or SE, depending on the data and the standard in the related literature, but I really don't know why the entire data set was not reported. Statistics may be used to summarize data, but when Table 1 draws from only 13 data points there does not seem to be any reason to not report them all.

Similarly, Table 2 reports statistics from only 8 data points. Here the means are reported, but no range. Curiously, the "Peak Thrust" (presumably the top of the range) is reported: better than nothing I suppose but worse than the range. Keeping in mind that I am not familiar with this area of research, and I have not read the paper in detail, I would recommend minor changes in the way the results are reported.

To barbos' complaint, upon further thought, I'm not certain they could have calculated error in any case. I previously said that error is a function of variance, which is true... and stipulated that there were too few measurements to calculate variance with any statistical credibility. Upon further reflection and thought, however, I realize that I was incorrect - to calculate error, you must have an expectation. It is my impression that NASA could not have had a calculated expected value for their measurements... since by all accounts it shouldn't work at all! And without an expected value, you can't calculate error from expected, right?

Or am I wrong?

I think that there might be a confusion about the term "error" here. In statistics, "error variance" refers to variance that is not associated with any of the independent variables considered. That is, it has nothing to do with "error" in the sense of "mistake". It was perhaps an unfortunately choice of terms, but it was coined and now we are stuck with it.

Peez

 

[barbos]

Really? And how about your resorting to years of experience?

First you said you had a course, now you say you are a PHD in statistics?

Nope, that's not what I said, You seem to be having reading comprehension problems.

The math of statistics is is not difficult. I spent several years in the 80s going through the books and coding algorithms on my first PC.

Resorting to your experience again?

I am not a PHD, I am autodidactic always exploring and self learning. Classes to me were always slow and tortuous. I am not dismissive of advanced degrees, but for me a PHD carries no special weight. Armed with undergrad math and science one can teach oneself and apply most anything.

I don't have a slightest interest in your life experiences, sorry.

---
more posturing and lecturing
---

I see nothing to comment here, so I just repeat again.

5 measurement is enough to estimate standard deviation and is done all the time. Everybody who has gone through undergraduate physics lab knows and literally has done it (estimating errors based on 5 measurements)

Yes, taking a few measurements and averaging is common. The SD gives you an idea of variability.

You are unable to support your 'good enough 'claim other than they do it in physics 101 labs?.

But again, how do you determine a sample size to meet a confidence level requirement? Do you even understand the question yes or no?.

It is covered in any basic text.

Taking a few measurements and averaging is descriptive.

Determining how you will sample to meet a measurement accuracy objective is not the same thing, as I determining the number of test runs in the OP paper.

You do not appear to understand the difference.

I receive a large crate of 1000 metal rods and I want to check against mean length specification. If I install them in a product and they are out of spec there will be financial issues. Would you just use 5 samples without thinking.? Another yes no question.

Resorting to my experience? Both experience and theory. herylone ledsto dangerous decisions. I refuted you with simple examples.

I like to use 20 as a min sample based on experience and theory. As N gets large normal statistics becomes a good approximation for parameters,.

I showed in my last post that when random sampling from an exponential distribution as N increases the distribution of sample means become normal, the CLT. A desirable condition.

http://en.wikipedia.org/wiki/Sample_size


When measuring a deterministic electrical signal corrupted by random noise we average measurements. The +- deviations about the mean average to zero. In the limit as n gets large the average approaches the true value of the signal, Law Of large Numbers.

Why are you throwing random and irrelevant to my postings crap?
Nothing you just posted has any relation to my post you quoted or even reality.
Do you even understand concept of discussion?

 

[barbos]

Let me get it straight. Someone who gets confused by the term "error" yet somehow sure that 5 events is not good statistics for SD?
Really?

There is less confusing word for it - "uncertainty", but it's a long word.

 

[beero1000]

Really? And how about your resorting to years of experience?

First you said you had a course, now you say you are a PHD in statistics?

Nope, that's not what I said, You seem to be having reading comprehension problems.

The math of statistics is is not difficult. I spent several years in the 80s going through the books and coding algorithms on my first PC.

Resorting to your experience again?

I am not a PHD, I am autodidactic always exploring and self learning. Classes to me were always slow and tortuous. I am not dismissive of advanced degrees, but for me a PHD carries no special weight. Armed with undergrad math and science one can teach oneself and apply most anything.

I don't have a slightest interest in your life experiences, sorry.

---
more posturing and lecturing
---

I see nothing to comment here, so I just repeat again.

5 measurement is enough to estimate standard deviation and is done all the time. Everybody who has gone through undergraduate physics lab knows and literally has done it (estimating errors based on 5 measurements)

Yes, taking a few measurements and averaging is common. The SD gives you an idea of variability.

You are unable to support your 'good enough 'claim other than they do it in physics 101 labs?.

But again, how do you determine a sample size to meet a confidence level requirement? Do you even understand the question yes or no?.

It is covered in any basic text.

Taking a few measurements and averaging is descriptive.

Determining how you will sample to meet a measurement accuracy objective is not the same thing, as I determining the number of test runs in the OP paper.

You do not appear to understand the difference.

I receive a large crate of 1000 metal rods and I want to check against mean length specification. If I install them in a product and they are out of spec there will be financial issues. Would you just use 5 samples without thinking.? Another yes no question.

Resorting to my experience? Both experience and theory. herylone ledsto dangerous decisions. I refuted you with simple examples.

I like to use 20 as a min sample based on experience and theory. As N gets large normal statistics becomes a good approximation for parameters,.

I showed in my last post that when random sampling from an exponential distribution as N increases the distribution of sample means become normal, the CLT. A desirable condition.

http://en.wikipedia.org/wiki/Sample_size


When measuring a deterministic electrical signal corrupted by random noise we average measurements. The +- deviations about the mean average to zero. In the limit as n gets large the average approaches the true value of the signal, Law Of large Numbers.

Why are you throwing random and irrelevant to my postings crap?
Nothing you just posted has any relation to my post you quoted or even reality.
Do you even understand concept of discussion?

:laughing-smiley-014

 

[steve_bnk]

Really? And how about your resorting to years of experience?

First you said you had a course, now you say you are a PHD in statistics?

Nope, that's not what I said, You seem to be having reading comprehension problems.

The math of statistics is is not difficult. I spent several years in the 80s going through the books and coding algorithms on my first PC.

Resorting to your experience again?

I am not a PHD, I am autodidactic always exploring and self learning. Classes to me were always slow and tortuous. I am not dismissive of advanced degrees, but for me a PHD carries no special weight. Armed with undergrad math and science one can teach oneself and apply most anything.

I don't have a slightest interest in your life experiences, sorry.

---
more posturing and lecturing
---

I see nothing to comment here, so I just repeat again.

5 measurement is enough to estimate standard deviation and is done all the time. Everybody who has gone through undergraduate physics lab knows and literally has done it (estimating errors based on 5 measurements)

Yes, taking a few measurements and averaging is common. The SD gives you an idea of variability.

You are unable to support your 'good enough 'claim other than they do it in physics 101 labs?.

But again, how do you determine a sample size to meet a confidence level requirement? Do you even understand the question yes or no?.

It is covered in any basic text.

Taking a few measurements and averaging is descriptive.

Determining how you will sample to meet a measurement accuracy objective is not the same thing, as I determining the number of test runs in the OP paper.

You do not appear to understand the difference.

I receive a large crate of 1000 metal rods and I want to check against mean length specification. If I install them in a product and they are out of spec there will be financial issues. Would you just use 5 samples without thinking.? Another yes no question.

Resorting to my experience? Both experience and theory. herylone ledsto dangerous decisions. I refuted you with simple examples.

I like to use 20 as a min sample based on experience and theory. As N gets large normal statistics becomes a good approximation for parameters,.

I showed in my last post that when random sampling from an exponential distribution as N increases the distribution of sample means become normal, the CLT. A desirable condition.

http://en.wikipedia.org/wiki/Sample_size


When measuring a deterministic electrical signal corrupted by random noise we average measurements. The +- deviations about the mean average to zero. In the limit as n gets large the average approaches the true value of the signal, Law Of large Numbers.

Why are you throwing random and irrelevant to my postings crap?
Nothing you just posted has any relation to my post you quoted or even reality.
Do you even understand concept of discussion?

Because you keep insisting 5 samples is 'generally good enough' without providing any actual usages where that would be true, and I keep providing examples and theory that shows you wrong.

Apparently your experience and knowledge is limited to calculating standard deviations, you say every day.

What do you do with those numbers, how are they used. What are the consequences of being off?

I'll provide an measurement example and you can respond, or not. Numbers trump words.

You do not appear to be able to discuss statistics being making a claim the face of refutation..

 

[Emily Lake]

I mostly skimmed the article, much of the technical aspects are beyond my understanding, but I did not see any reason that the sample sizes were so low and so my first thought (apart from adjusting to the use of English measurements in a published paper) was that they should have completed more replicates. Another issue that I noticed was statements such as "Based upon this observation, both test articles (slotted and unslotted) produced significant thrust in both orientations (forward and reverse)." without any basis for determining that the results were significant (statistically or experimentally).

That being said, Table 1 does present ranges, which one might argue to be appropriate in this case (given the sample sizes). An argument might be made to report SD, or SE, depending on the data and the standard in the related literature, but I really don't know why the entire data set was not reported. Statistics may be used to summarize data, but when Table 1 draws from only 13 data points there does not seem to be any reason to not report them all.

Similarly, Table 2 reports statistics from only 8 data points. Here the means are reported, but no range. Curiously, the "Peak Thrust" (presumably the top of the range) is reported: better than nothing I suppose but worse than the range. Keeping in mind that I am not familiar with this area of research, and I have not read the paper in detail, I would recommend minor changes in the way the results are reported.

Honestly, the majority of the article was so far beyond my bailiwick that I couldn't do much more than latch on to the fact that tables existed and contained some numbers being reported in a particular fashion . I could only assume that there exists some valid reason why they could not take many, many more measurements. I don't know what that reason is, and I can't read the tehcnical jargon of the paper well enough to find that reason, so I'm left with an assumption. Maybe it's a bad assumption.

To barbos' complaint, upon further thought, I'm not certain they could have calculated error in any case. I previously said that error is a function of variance, which is true... and stipulated that there were too few measurements to calculate variance with any statistical credibility. Upon further reflection and thought, however, I realize that I was incorrect - to calculate error, you must have an expectation. It is my impression that NASA could not have had a calculated expected value for their measurements... since by all accounts it shouldn't work at all! And without an expected value, you can't calculate error from expected, right?

Or am I wrong?

I think that there might be a confusion about the term "error" here. In statistics, "error variance" refers to variance that is not associated with any of the independent variables considered. That is, it has nothing to do with "error" in the sense of "mistake". It was perhaps an unfortunately choice of terms, but it was coined and now we are stuck with it.

Peez

<giggle> I see what I did. I was thinking of error in terms of goodness of fit to a model. That is not what is being discussed here, so I'm completely off base. Never mind. I have educated myself.

 

[skepticalbip]

Honestly, the majority of the article was so far beyond my bailiwick that I couldn't do much more than latch on to the fact that tables existed and contained some numbers being reported in a particular fashion . I could only assume that there exists some valid reason why they could not take many, many more measurements. I don't know what that reason is, and I can't read the tehcnical jargon of the paper well enough to find that reason, so I'm left with an assumption. Maybe it's a bad assumption.

My reading of the article is that it was just a test report. The test being to determine if there was anything to the claim by the Chinese that thrust could be generated by this contraption. They stated that they would not try to explain the physics involved. It seems that they took sufficient data to accomplish this limited test goal of determining a yes/no answer. If the intent had been to plot thrust vs. power vs. frequency or to determine the physics involved then they would have needed many, many more data points.

I haven't noted that Barbos has criticized the actual test methodology, only criticizing the composition of the test report as though it was a paper presented for publication in a major journal with him as referee. Being a math major, he seems to insist on specific statistical analysis of the data (whether or not it is meaningful to the intent of the test). I suppose an English major as referee would be criticizing the syntax and sentence structure of the report.